高校数学B「統計的な推測」 第2章｜確率変数の期待値・分散・標準偏差をやさしく解説

期待値や分散について理解してそれを実際に求めることは、
統計的な推測を学ぶ上での最初の山場です。

この記事では、「期待値・分散・標準偏差」の意味を徹底解説します。
さらに例題を通して実際に値を求める方法もお伝えします。。

このような疑問を持つ高校生・受験生の方は、ぜひここで基礎を固めて、
共通テスト数学の点数アップにつなげましょう！

期待値・分散・標準偏差とは？

まずはそれぞれの用語が何を意味するものなのか、
ざっくりとしたイメージを持ちましょう。

それぞれの語句についてもう少しだけ肉付けをします。

期待値とは？

期待値（Expected Value）とは、起こりうる値の「平均」のことです。

10%の確率で100円をもらえる場合：

期待値は、$100 \times \frac{1}{10} = 10 (円)$ です。

分散とは？

分散（Variance）とは、平均からの「ブレの大きさ」を表す数値です。

平均身長が170cm のクラスが２組あったとき：

この時、分散がより大きいクラスの方が、
生徒一人ひとりの身長のばらつきが大きくなっています。

分散のイメージをさらに深めたい方は
「分散が100から分かること」コラムをチェックしてください！

標準偏差とは？

標準偏差とはブレの大きさを元の単位で表した数値です。

ここでは分散の平方根の値、
と覚えておけば大丈夫です。

「標準偏差ってあえて覚える必要ある？」と違和感を感じ方は、
「標準偏差はなぜ必要？分散だけではダメなのか」のコラムを読んで解消しましょう。

期待値・分散・標準偏差。

これらの語句は統計的な推測の単元全体で何度も登場します。

それぞれの語句についてしっかりと意味を理解して、
違和感はここで解消しておきましょう！

期待値・分散・標準偏差の公式

続いて、期待値・分散・標準偏差の公式を紹介します。

それぞれの語句について、それが表す意味と公式の形をリンクさせましょう！

期待値の公式

（確率変数X がとる値 $x_i$） × （それが起こる確率 $P(x_i)$）
これをすべて足し合わせることで求めます。

分散の公式

確率変数Xがとる値 $x_i$ と平均 $E[X]$との差を二乗して
それが起こる確率をかけてから足し合わせることで求めます。

分散の公式は期待値のものと比べると、
式が複雑で計算の理由も分かりにくいですね。

分散の公式がなぜこのような形をしているのか気になる方は、
「分散の意味と誕生エピソード」のコラムをチェックしてください。

分散については、もう一つの型も覚えましょう。

二乗の平均 － 平均の二乗 の形

確率変数X² の期待値 $E[X^2]$ から、確率変数X の期待値を二乗した値 $(E[X])^2$ を引くことで
分散の値を求めることができます。

実際に分散を計算する際は、
定義の形よりもこちらの形を用いる方が計算が楽になることが多いです。

この公式の導出方法が気になる方は、以下の記事で確認してください。

高校数学B「統計的な推測」 分散の公式の導出法をやさしく解説

標準偏差の公式

標準偏差は分散の平方根です。

分散の公式が覚えられれば、標準偏差は簡単ですね！

ここまでで期待値・分散・標準偏差について
簡単なイメージとそれぞれの公式を紹介しました。

ここからは実際に、それぞれの値を計算してみましょう！

例題：分散・標準偏差を求めよう

期待値・分散・標準偏差について実際に具体例で求めてみましょう！

期待値・分散・標準偏差を求めるためには、確率分布を表にまとめるスキルが必須です。
確率分布のまとめ方が不安な方は、先に第１章を読んで復習をしてください！

高校数学B 「統計的な推測」 第1章｜確率変数と確率分布をやさしく解説

第１章「確率変数と確率分布」と同様に、

サイコロ
コイン
じゃんけん

のそれぞれを題材とした例題を解説します。

サイコロの場合

手順に従って例題をクリアしましょう。

確率変数を定義・取りうる値を考える

確率変数X はサイコロの出目ですね。

$X=\{1, 2, 3, 4, 5, 6\}$

確率分布を表にまとめる

X	$1$	$2$	$3$	$4$	$5$	$6$	計
P	$\dfrac{1}{6}$	$\dfrac{1}{6}$	$\dfrac{1}{6}$	$\dfrac{1}{6}$	$\dfrac{1}{6}$	$\dfrac{1}{6}$	$1$

確率分布を表にまとめる方法は第１章ですでに解説をしました。
ここではかんたんに結果のみ。

E[X], E[x²] を計算する

先ほどまとめた表を使って計算をします。

まずはE[X], E[x²]について計算。

E[X] とは確率変数X の期待値
E[X²]とは確率変数X の取り得る値をすべて二乗にして期待値を計算した値です。

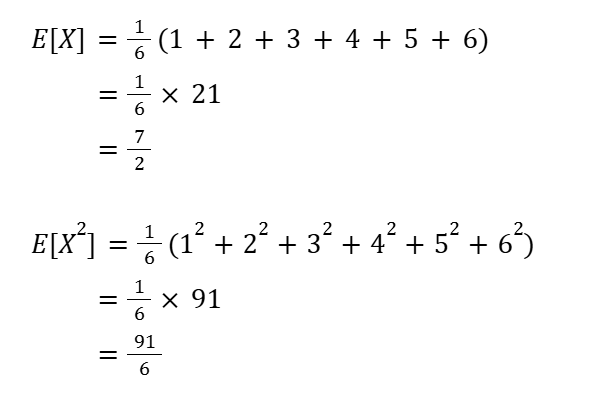
期待値・分散・標準偏差を求める

続いて、公式から期待値・分散・標準偏差を求めます。

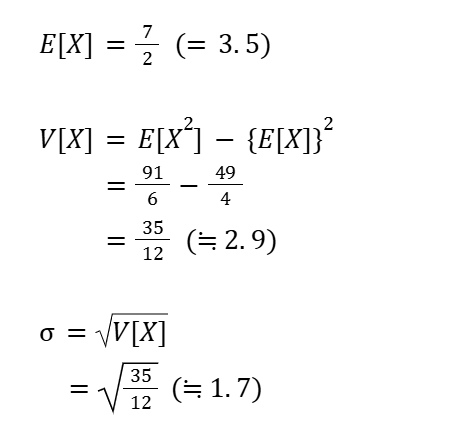
E[X] … 期待値
V[X] … 分散
σ … 標準偏差

これでクリアです。

E[X], V[X], σ が何を表すかはここで覚えましょう！

コインの場合

この問題についても、先ほど同じで準で解きます。

確率変数を定義・取りうる値を考える

確率変数X は表のコインの枚数。

$X=\{0, 1, 2\}$

確率分布を表にまとめる

X	$0$	$1$	$2$	計
P	$\dfrac{1}{4}$	$\dfrac{2}{4}$	$\dfrac{1}{4}$	$1$

E[X], E[x²] を計算する

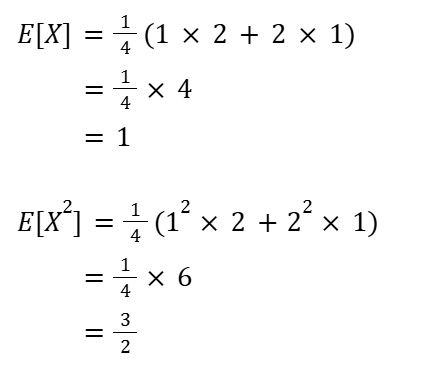
期待値・分散・標準偏差を求める

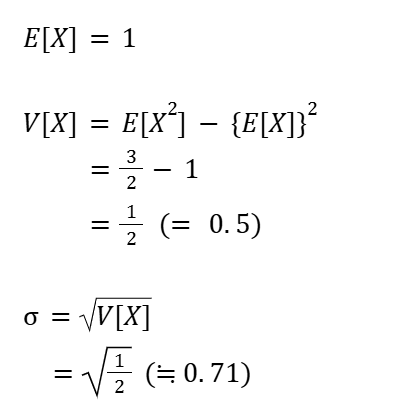
これでクリア！

じゃんけんの場合

確率変数を定義・取りうる値を考える

確率変数X は、じゃんけんの勝者の人数。

$X=\{0, 1, 2\}$

確率分布を表にまとめる

X	$0$	$1$	$2$	計
P	$\dfrac{1}{3}$	$\dfrac{1}{3}$	$\dfrac{1}{3}$	$1$

E[X], E[x²] を計算する

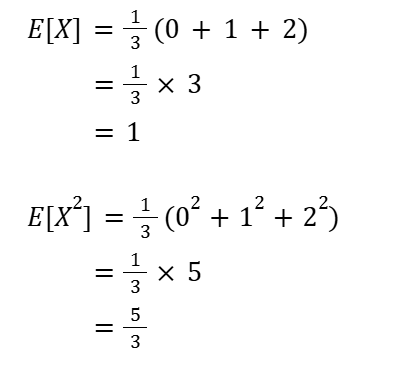
期待値・分散・標準偏差を求める

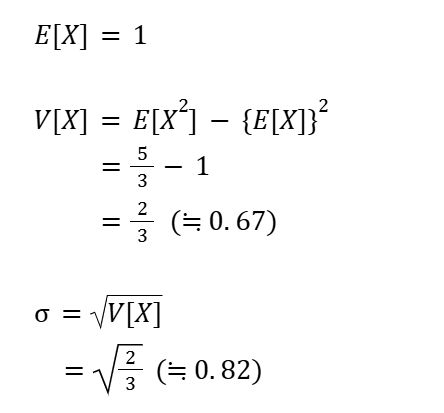
これでクリア！

解法の手順

どの例題についても、同じ手順を用いて解きました。

この手順を再度確認したら、演習へ進みましょう！

演習

解法の確認

この手順で解くことを意識してください。

確率変数の定義と取りうる値を考える

表が出る枚数を確率変数Xとする。

$X=\{0, 1, 2, 3\}$

確率分布を表にまとめると

X	$0$	$1$	$2$	$3$	計
P	$\dfrac{1}{8}$	$\dfrac{3}{8}$	$\dfrac{3}{8}$	$\dfrac{1}{8}$	$1$

E[X], E[x²] を計算

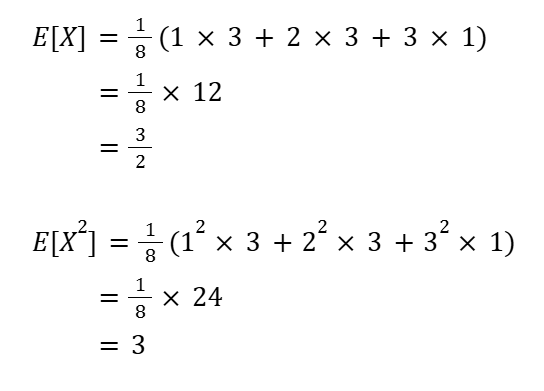
期待値・分散・標準偏差を求める

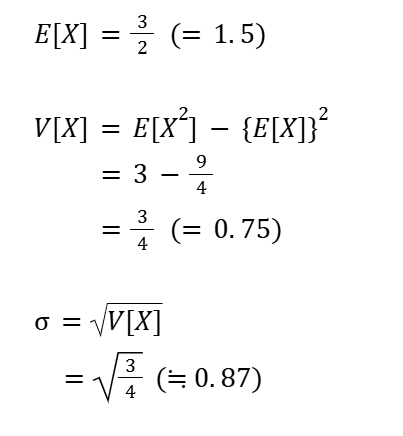
まとめ

期待値・分散・標準偏差についてよく理解できましたか？

それぞれの用語のイメージは必ずつかんでおきましょう。

その上で、これらを実際に求めるために用いる公式を覚えましょう。

余力のある方は分散のコラムや、分散の計算式の証明をチェックしておくと◎です。

次回は「何を確率変数X でとるか」についてさらに踏み込みます。

複雑な設定の問題では、
問われているものを直接確率変数X でとってしまうと、その後の処理が大変なことに…

そんな時に役立つのが「第３章｜確率変数の変換 Y = aX + b の期待値・分散」で学ぶ内容です！

期待値と分散・標準偏差の確認テスト｜この章の理解はバッチリ？

以下のポイントが自力で説明・再現できれば、この章はほぼマスターです！

• 期待値・分散・標準偏差とは何か
• 期待値・分散・標準偏差の公式を説明できるか
• 確率分布をまとめて、そこから期待値・分散・標準偏差が求められるか

「ちょっと怪しいかも…」と思った箇所があれば、上に戻って再チェックしてみましょう！

---

◀ 第１章｜確率変数と確率分布

▶ 第３章｜確率変数の変換 Y = aX + b の期待値・分散

▶︎ 高校数学B「統計的な推測」シリーズ目録・過去問解説のまとめはこちら！

---

共通テストに不安がある方は、お気軽にご連絡ください。

無料のオンライン学習相談・体験授業をご用意しています！

▶︎ [公式LINEに登録する]
▶︎ [お問い合わせフォームへ]