高校数学B 「統計的な推測」 第1章|確率変数と確率分布をやさしく解説

統計的な推測は、高校数学Bの中でも、共通テストで得点を伸ばすうえで非常に重要な単元です。
このページでは、「確率変数」や「確率分布」の基本を、例題を通してわかりやすく解説します。
- 「確率変数って何?」
- 「確率分布って何?」
- 「確率分布ってどうやって計算するの?」
このような疑問を持つ高校生・受験生の方は、ぜひここで基礎を固めて共通テスト数学の点数アップにつなげましょう!
確率変数・確率分布とは?

まずはそれぞれの用語についてざっくりとした認識を持ちましょう。
- 確率変数:起こり得る結果に、数を対応させたもの
- 確率:その結果が起こる「見込み」の強さを数で表したもの
- 確率分布:その「起こる可能性」を全体として一覧にしたもの
確率変数・確率分布は、日常生活ではあまり聞きなじみがない用語ですね。
これらの用語が何を指しているのか正しくつかむことが、統計的な推測を学習する第一歩目です!
確率変数・確率分布が何を指しているのか、はっきりとしたイメージを持つために
具体例を用いて確認をしていきましょう!
確率変数・確率分布って具体的に何?

確率変数・確率分布について具体例を通して学びましょう。
- サイコロ
- コイン
- じゃんけん
試験や問題でよく問われる、これら三つの例を用いて具体的に解説します。
それぞれの例について、
確率変数を定義する
確率分布を表にまとめる
これらを実践して理解を深めましょう!
サイコロの場合
確率変数を定義する
確率変数とは「起こり得る結果に、数を対応させたもの」でしたね。
1つのサイコロを投げて起こり得る結果は、
1の目が出る
2の目が出る
3の目が出る
4の目が出る
5の目が出る
6の目が出る
これら6通りですね。
サイコロは出目がすでに数値なので、
出目を絡めた確率変数を定義することを考えましょう。
例えば:
サイコロを1個投げた時に出る目の値
サイコロを3個投げた時に、偶数の目が出るサイコロの個数
サイコロを100回投げた時に出る目の値の平均値
これらはすべて確率変数です。
このように、確率変数の取り方は無数にあることを覚えておきましょう。
これらのうちから、
「サイコロを1個投げた時に出る目の値」
この確率分布をまとめてみましょう。
確率分布を表にまとめる
確率分布とは、その「起こる可能性」を全体として一覧にしたものでした。
確率変数X を「サイコロを1個投げた時に出る目の値」として、
確率分布を表にまとめなさい。
これを例題として実際に確率分布をまとめましょう。
まずは確率変数X の取り得る値の確認から。
X はサイコロの出目の値なので、
となります。
確率変数X の分布について、表にしてまとめましょう。
| X | 計 | ||||||
|---|---|---|---|---|---|---|---|
| P |
このように確率分布を表にまとめられればクリア。
コインの場合
確率変数を定義する
確率変数とは「起こり得る結果に、数を対応させたもの」です。
コインを投げて起こり得る結果は、
表が出る
裏が出る
の2通りですね。
表・裏は数値ではないことに注意。
これらを数値化することで確率変数として扱います。
例えば:
コインを1回投げた時に、表が出たコインの枚数
コインを10枚投げた時に、表が出たコインの枚数
10円硬貨を10枚投げた時に、表が出たコインの合計金額
コインを100回投げた時に、表が出た回数の平均値
サイコロ同様に、確率変数の取り方は無数にあることを覚えておきましょう。
これらのうちから、
「サイコロを1個投げた時に出る目の値」
これについて確率分布をまとめてみましょう。
確率分布を表にまとめる
確率分布とは、その「起こる可能性」を全体として一覧にしたものでした。
コインを1回投げたとき、表の出る回数について確率分布をまとめなさい。
コインを1回投げて表が出る回数は
0回か1回です。
よって、コインを1回投げたときの表の出る回数を確率変数X とすると、
となります。
確率変数X の分布について、表にしてまとめましょう。
| X | 計 | ||
| P |
このように確率分布を表にまとめられればクリア。
じゃんけんの場合
確率変数を定義する
確率変数とは「起こり得る結果に、数を対応させたもの」です。
じゃんけんをして起こり得る結果は、
勝つ
負ける
あいこ
の3通りですね。
勝つ・負ける・あいこは数値ではないので、
これらを数値化することで確率変数として扱います。
例えば:
3人でじゃんけんを1回した時に勝つ人数
2人でグリコのじゃんけんを5回した時に、勝者が進んだ歩数
2人でじゃんけんを100回繰り返した時に、あいこになる回数の平均値
じゃんけんもやはり、確率変数の取り方は無数にあります。
これらのうちから、
「3人でじゃんけんを1回した時に勝つ人数」
これについて確率分布をまとめてみましょう。
確率分布を表にまとめる
確率分布とは、その「起こる可能性」を全体として一覧にしたものでした。
3人でじゃんけんを1回した時に勝つ人数を、確率変数X とする。
確率変数X について確率分布をまとめなさい。
3人でじゃんけんを一回した時の結果は
勝者0人(あいこ)
勝者1人(1人勝ち)
勝者2人(2人負け)
となります。
確率変数X の分布について、表にしてまとめましょう。
今回は確率の計算が難しいですね。
| X | 計 | |||
| P |
このように確率分布を表にまとめられればクリア。
確率変数を定義する
確率分布を表にまとめる
これら二つについて、具体例を用いて解説を行いました。
いずれの具体例も
- 確率変数を定義する
- 確率変数の取りうる値を考える
- 確率分布を表にまとめる
この手順で処理をを行いました。
次は演習を通して、確率分布を自力で表でまとめてみましょう!
演習

ここでは、実際の演習を通して、問題の解き方・手順について見ていきましょう。
箱の中に白い球が3つ、赤い球が2つ入っている。
この箱から同時に球を3つ取り出すとき、出る赤玉の数をXとする。
このとき、確率変数Xの確率分布を求めよ。
解法
確率変数を定義する
この操作で取り出す赤玉の個数を、確率変数X とします。
確率変数の取りうる値を考える
確率変数Xの取りうる値について考えます。
同時に球を3つ取り出す
ということは、X = {1, 2, 3} かな…
と思った方! これは×です。
確率変数X は「取り出した赤玉の個数」でしたね。
箱の中に入っている赤玉は2つ。
X の最大値2です。
X = 3 は取れません。
さらに…
取り出した3つの球がすべて白であることもあります。
つまりX = 0 も起こりえます。
よって確率変数X の取りうる値は
X = {0, 1, 2}
です。
確率分布を表にまとめる
次に、確率分布を表にまとめます。
実際の演習では、表の枠を作るところから自分で行います。
確率変数がとり得る値についてはすでに考えているので、
それをもとに先に表を作ってしまいましょう。
| X | 計 | |||
| P |
このように、確率は空欄の状態で表を作ります。
そしてこの空欄に、確率を計算して当てはめていきます。
まずは分母から:
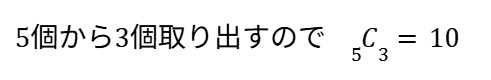
つぎに分子:
まずは確率変数の値ごとに、実際に取り出す赤玉の個数・白玉の個数を整理しましょう。
| X | 赤玉(2個中) | 白玉(3個中) |
| 0 | 0 | 3 |
| 1 | 1 | 2 |
| 2 | 2 | 1 |
例えばX = 0 を取るとき、
赤玉を2個中0個・白玉を3個中3個取り出すということ。
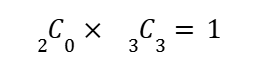
同様に考えると、X = 1 を取るとき、
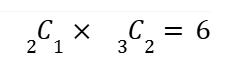
X = 2 を取るとき、
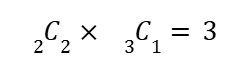
それぞれの確率変数を取る確率を表に書き込むと…
| X | 計 | |||
| P |
このように確率分布を表にまとめられればクリア。
確率の値は約分できる場合もそのままにして、
各値の分母をそろえておきましょう。
- 確率変数を定義する
- 確率変数の取りうる値を考える
- 確率分布を表にまとめる
例題と同じ手順で、演習題を解くことができました。
この手順をしっかりと覚えて、演習をさらに重ねましょう!
まとめ
確率変数・確率分布について具体例も交えて解説を行いました。
確率分布を表にまとめる手順はしっかりと覚えておきましょう。
例題・演習以外の問題についても、
自力で確率分布をまとめる練習を重ねてください。
次回は「第2章|期待値と分散・標準偏差」です。
確率変数・確率分布の確認テスト|この章の理解はバッチリ?
以下のポイントが自力で説明・再現できれば、この章はほぼマスターです!
- 確率変数とは何か?サイコロ・コイン・じゃんけんの例で説明できるか
- 確率分布とは?表の構造や意味を理解しているか
- 自分で表をつくり、確率を計算できるか
「ちょっと怪しいかも…」と思った箇所があれば、上に戻って再チェックしてみましょう!
▶第2章|期待値と分散・標準偏差
▶︎ 高校数学B「統計的な推測」シリーズ目録・過去問解説のまとめはこちら!
共通テストに不安がある方は、お気軽にご連絡ください。
無料のオンライン学習相談・体験授業をご用意しています!



“高校数学B 「統計的な推測」 第1章|確率変数と確率分布をやさしく解説” に対して5件のコメントがあります。
コメントは受け付けていません。