大学入学共通テスト2025年度 追試験 解説【統計的な推測】【数学Ⅱ・数学B・数学C】

2025年度大学入試共通テスト追試験(数学ⅡBC)で出題された「統計的な推測」について、全設問を順番にやさしく丁寧に解説します。
試験問題の概要
各設問の解説
解くために必要な考え方・公式
単元ごとの復習ポイント
これらについて分かりやすくまとめています。
大学入試・共通テスト・学校の定期テスト対策にご活用ください。
▶︎ 統計的な推測を最初から整理したい方はこちら(シリーズ目録)
試験問題の概要

2025年度の追試験のテーマは、くじ引きによる得点でした。
くじ引きの得点を確率変数X
得点から参加費を引いた損得点を確率変数Y
と定義して、くじ引きによる得点・損得点について考える問題です。
大きな流れは次の3段階です。
① 確率変数X, Y について整理(確率分布・期待値・分散)
- 確率分布を表にまとめる
- 確率変数 の期待値と分散
② ある事象の起こる確率を考察する(標本平均・正規分布)
- くじ引きを400回繰り返したときに、損得点Y の合計が0以上になる確率
③ 一部のデータをもとに母平均を推定(区間推定)
- くじ引き400回の結果から、母平均を推定
題材は比較的スタンダードです。
「たくさんあるもの」についてではなく、
「たくさん行った結果」についての問題。
設問は、やはり追試験だけあって難しめです。
1題目は典型的な問題
2題目は頻出問題の混合問題
3題目は道中の処理が珍しい
どの場面でどの手法を使うか
各場面で問われていることとその解決策
こちらを意識しながら読み進めてみてください!
問題の解説

① 確率変数X, Y について整理(確率分布・期待値・分散)
ア … 1
イ … 8
ウ … 8
エ … 9
オ … 2
カ … 0
キ … 2
ク … 5
ケ … 1
コ … 0
📘解説
「000」から「999」の合計1000枚のカードから1枚引く。
- 番号が「777」 … 2000点
- 番号の下二桁が「22」 … 800点
- 番号の下一桁が「1」 … 100点
- 上記以外 … 0点
このルールで得られる得点を確率変数X として、確率分布を表にまとめます。
| X | 2000 | 800 | 100 | 0 | 計 |
| P | 1/1000 | 10/1000 | 100/1000 | 889/1000 | 1 |
このうち
P(X = 800) = 1/100
P(X = 0) = 889/1000
が設問として問われていました。
表をもとに期待値の計算。
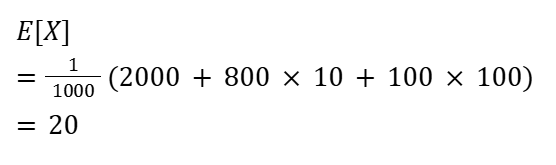
分散V(X) = 11000
は問題文の中で与えられていました。
これで確率変数X については完了!
くじ引きを1回引くたびに25点引かれる
という条件を追加して点数を考えます。
この時の損得点を確率変数Y として、
Yの期待値・分散を求めます。
c = 25 とします。
Y = X -25 (つまりY = X – c)とおくと
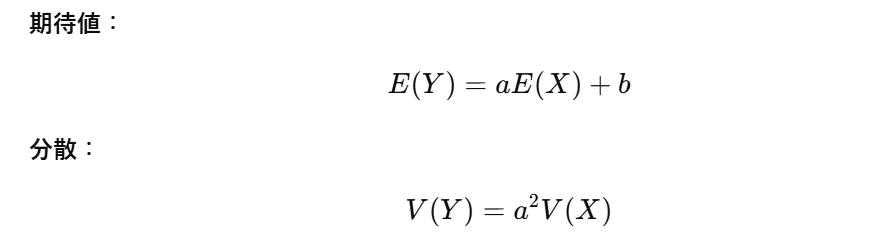
確率変数の変換の公式を用いて、Yの期待値・分散を求めることができます。
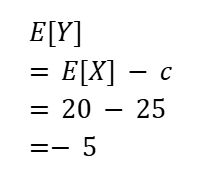
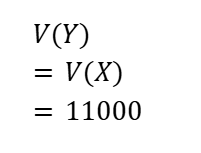
これで確率変数Y についてもクリア。
🧩解答に必要な考え方・公式
解説で用いた考え方・公式をまとめています。
不安のある単元は復習しましょう!
確率分布
確率変数の変換
② ある事象の起こる確率を考察する(標本平均・正規分布)
サ … 5
シ … 0
📘解説
くじ引きを400回行ったときの損得点Y₁, Y₂, … を
母平均E[Y], 母標準偏差√V(Y) の母集団から
無作為に抽出した大きさ400の無作為標本とみなす。
このように捉えることで
くじ引きを400回繰り返したときの損得点と、標本平均がつながります。
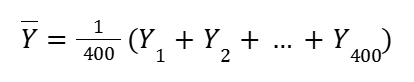
よって、
くじ引きを400回繰り返したときに、損得点Y の合計が0以上になる確率は
標本平均が0以上になる確率
と置き換えることができます。
また、標本の大きさ400は十分に大きいことから

ということが分かります。
E[Y], V(Y) を数値化すると

となります。
標本平均が0以上になる確率は正規分布表を用いて求められますね。
正規分布表を用いるために、確率変数を標準化しましょう。
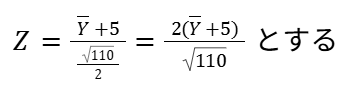
これでようやく解くことができます!
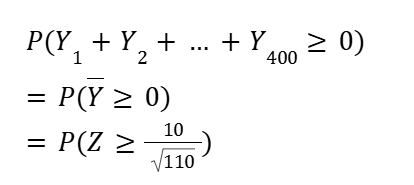
問題文中に √110 = 10.5 とする指示があるので
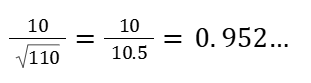
正規分布表の0.95 の値を確認しましょう。

f(0.95) = 0.3289 なので
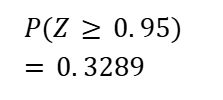
設問は、損得点Y の合計が0以上になる確率を選択肢から選ぶ形式でした。
算出した0.3289 に最も近い0.33 が答えです。
10/√110 を近似で0.95としたため、算出した値は答えとぴったりにはなりません。
標本平均と正規分布表の活用。
どちらも単体では頻出ですが、
これらが融合して一つの問題になっているのが本設問でした。
各タイミングで行うべきことを把握することが重要です。
🧩解答に必要な考え方・公式
解説で用いた考え方・公式をまとめています。
不安のある単元は復習しましょう!
標本平均
正規分布
標準化
③ 一部のデータをもとに母平均を推定(区間推定)
ス … 1
セ … 2
導入の問題です。
くじ引き3回で1,000点得点した人があらわれたので、その確率を考えてみます。
こちらは計算で求めましょう。
くじを3回引いて1,000点を得るためには
800点を1回、100点を2回
引く必要があります。
この確率を計算すると…
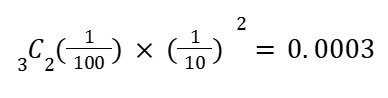
純粋な確率の問題が問われることもあるので注意しておきましょう!
くじを3回引いて1,000点が出る確率は計算上非常にまれなはず。
このような事象が起きたことから、
「くじの設定どおりに行われていないのではないか」
という疑問が生まれました。
この疑問を解決するために、
くじ引きの結果から母平均の95%信頼区間を推定して、E[X] がそれに含まれているのかを確認する。
これがこの問題の背景です。
もしもE[X] が区間に含まれていない場合は、
「くじの設定どおりに行われていない」と言える
という発想です。
くじを400回引いた結果を、
母平均m、母標準偏差σ の母集団から無作為に抽出した標本の大きさ400 の無作為標本
とします。
くじを400回引いた結果
得点の平均は16.75 点
標本の標準偏差は75点
「統計的な推測」の試験では母標準偏差が与えられていることが多いのですが、
今回分かっているのは標本標準偏差のみ。
「一般に、標本の大きさが十分に大きいときには、母標準偏差の代わりに、標本の標準偏差を用いてよい」
この処理が、他の年度の過去問と比べると珍しいですね。
問題文の指示に従って、σ = 75 ということにしましょう。
あとは計算するのみ。
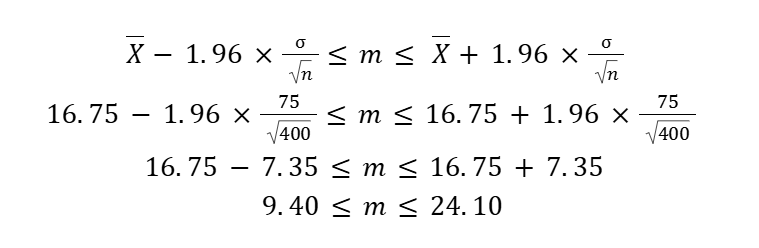
E[X] は 20 なので
この区間に入っていることが確認できました。
これでクリア!
🧩解答に必要な考え方・公式
解説で用いた考え方・公式をまとめています。
不安のある単元は復習しましょう!
母平均の推定
~準備中~
仮説検定
~準備中~
まとめ
追試験はやはり本試験と比べると少し難しい印象ですね。
2題目の融合問題は演習する価値が特に高い問題です。
今回のように複数の処理が混ざった問題を解くことで、
ひとつひとつの考えがより深まります。
随所に現れる確率の計算は、むしろラッキー問題と感じられるように対策をしましょう!
▶︎ 統計的な推測を最初から整理したい方はこちら(シリーズ目録)
共通テスト・大学入試に向けて勉強を始めたい方は、林個別指導中にお問い合わせください。
無料のオンライン体験授業も用意しております!


