【高校受験】文字式の利用 記述問題の書き方【中学数学まとめ】

この記事では、文字式の利用 記述問題の書き方について解説をします。

教科書レベルの頻出問題を例題として、解法の流れを徹底解説！

問題を系統ごとに整理して、高校受験に向けての土台を作りましょう！

文字式の利用 記述問題の頻出パターン

文字式の利用 記述問題の頻出パターンは以下の２通りです

1. 数の規則性
2. 図形の規則性

それぞれについて定番の問題と、その解法を整理しましょう。

数の規則性

例題１…中学２年生
例題２…中学３年生
例題３…中学２年生

で学習する問題です。

いずれの問題も記述の書き方の骨格は同じです。

解説を通して、数の規則性の記述問題の書き方を学びましょう！

例題１の解説

1.扱いたい数について、文字式で表す

まずは連続する３つの整数を、文字式で表します。

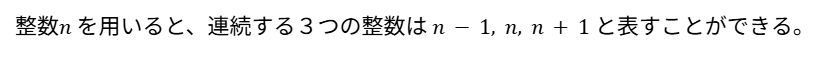
※連続する３つの整数はn, n+1, n+2 ではなく
今回のようにn-1, n, n+1 と表すと
この後の処理が楽になります！

2.数同士の関係について、文字式で表す

次は連続する３つの整数の和を、文字式で表します。

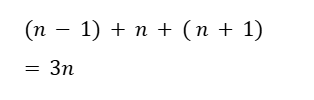
3.証明したいことについて、文字式で表す

次は連続する３つの整数の和が３の倍数であることを、文字式で表します。

すでに連続する３つの整数の和までは求めているので、
これが３の倍数になることが言えればオーケーです。

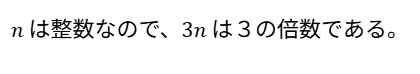
※n が整数なので、3n （つまり3 × n） は３の倍数であることを書きましょう。

4.仕上げ

最後に、証明したことをもう一度書いて終了です。

※ここは問題文をそのまま写せば問題なしです！

解法のまとめ

1. 扱いたい数について、文字式で表す
2. 数同士の関係について、文字式で表す
3. 証明したいことについて、文字式で表す
4. 仕上げ

例題２，３についてもこれと同じ骨格の解答を目指しましょう！

例題２の解説

1.扱いたい数について、文字式で表す

まずは連続する３つの整数を、文字式で表します。

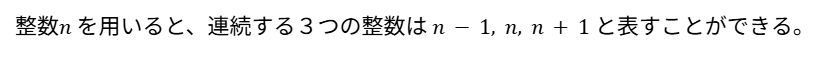
※ここは例題１と同じ！

2.数同士の関係について、文字式で表す

次は最も大きい数の平方と最も小さい数の平方の差を、文字式で表します。

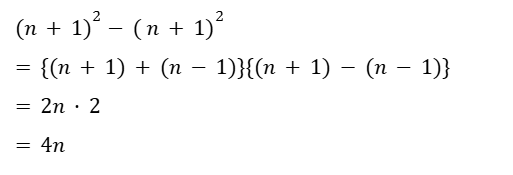
※ここの計算過程で多項式の展開・因数分解の考えを用います

3.証明したいことについて、文字式で表す

最も大きい数の平方と最も小さい数の平方の差が、真ん中の数の４倍になることを文字式で表します。

すでに最も大きい数の平方と最も小さい数の平方の差までは求めているので、
これが真ん中の数の４倍になることが言えればオーケーです。

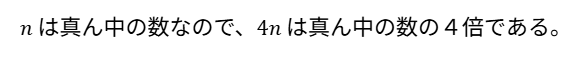
※証明したい内容によっては、「nは整数なので～」以外のパターンがあることを覚えておきましょう。

4.仕上げ

最後に、証明したことをもう一度書いて終了です。

※ここは問題文をそのまま写せば問題なしです！

解法のまとめ

1. 扱いたい数について、文字式で表す
2. 数同士の関係について、文字式で表す
3. 証明したいことについて、文字式で表す
4. 仕上げ

一つ一つの段階で行う具体的な作業は多少変わりますが
記述の流れは例題１と同じ！

例題３の解説

1.扱いたい数について、文字式で表す

まずは二桁の自然数について、文字式で表します。

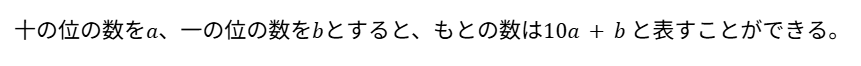
さらに、十の位と一の位を入れ替えた数についても、文字式で表します。

※文字式で表すものがひとつとは限らない！

2.数同士の関係について、文字式で表す

次はこの整数の十の位の数と一の位の数を入れ替えた数と、もとの整数の和を、文字式で表します。

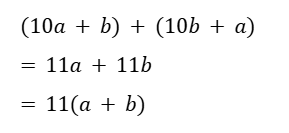
※共通因数である11でくくりましょう！
これができていると次への流れがスムーズです。

3.証明したいことについて、文字式で表す

この整数の十の位の数と一の位の数を入れ替えた数と、もとの整数の和が
11の倍数であることを文字式で表します。

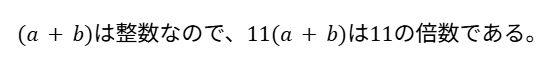
※「○○は整数なので～」のパターンは非常に多いです！

4.仕上げ

最後に、証明したことをもう一度書いて終了です。

※ここは問題文をそのまま写せば問題なしです！

解法のまとめ

数の規則性 記述問題の書き方の流れ

今回扱った３種類の例題はどれも同じ解法で証明することができます。

この解法の流れを覚えて、初見の問題に対しても使えるように練習をしましょう！

図形の規則性

例題１…中学２年生
例題２…中学３年生
で学習する問題です。

それぞれの例題を通して、記述問題の書き方を学びましょう！

数の規則性と同様に、どのパターンもできるだけ同じように解くということを意識してください。

例題１の解説

1.扱いたいものについて、文字式で表す

まずはもとの円錐の体積Vを、文字式で表します。

続いて、底面の半径を2倍、高さを1/4倍した円錐の体積を文字式で表します。

※与えられた文字a, h を使って
証明したい等式に絡む文字V, V’ を表しましょう

2.証明したい等式の各辺について、文字式で表す

（左辺である）V =
（右辺である）V ‘=

これらを文字式で表します。

※今回はどちらもすでに表せているので、ここでの処理はスルー

3.仕上げ

ここまでですでに、左辺と右辺を文字で表せているはずです。

最後に改めて、左辺 = 右辺であることを書きましょう。

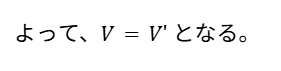
解法のまとめ

1. 扱いたいものについて、文字式で表す
2. 証明したい等式の各辺について、文字式で表す
3. 仕上げ

問題によっては手順１が難しいですが、
それを乗り越えられればあとはスムーズです！

例題２の解説

1.扱いたいものについて、文字式で表す

まずは道の面積S を、文字式で表します。

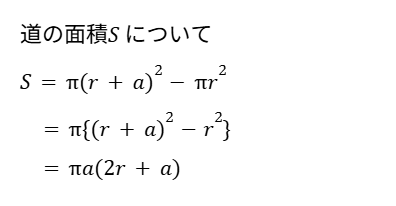
続いて、道の真ん中を通る線の長さl を文字式で表します。

※与えられた文字a, r を使って
証明したい等式に絡む文字S, l を表しましょう

2.証明したい等式の各辺について、文字式で表す

（左辺である）S =
（右辺である）al=

これらを文字式で表します。

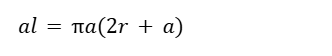
※左辺はすでに表せているので、ここでは右辺のみ処理

3.仕上げ

最後に改めて、左辺 = 右辺であることを書きましょう。

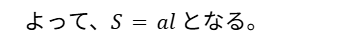
解法のまとめ

図形の規則性 記述問題の書き方の流れ

この解法の流れを覚えて、初見の問題に対しても使えるように練習をしましょう！

まとめ

数の規則性と図形の規則性。

これらについて、記述問題の書き方を解説しました。

まずは教科書レベルの頻出問題から記述の書き方の流れをつかみましょう。

繰り返し練習して基礎が固まったら、過去問にチャレンジしてください！

中学数学まとめシリーズについて

中学1年生から3年生の学校の授業では、数学の各分野について少しずつ分けて学習をしています。

学年ごとに段階を踏んで初見学習を消化できる一方、
同じ分野の内容なのにバラバラに覚えてしまうというデメリットもあります。

初見学習を終えた中学生が分野ごとに知識や考え方を改めて整理すること、
これが中学数学まとめシリーズの狙いです。

頭の中で別のものとして覚えてしまっている知識や解法を統合して、
受験に向けてより強い基盤を作りましょう！