【完全版】2025年(令和7年度) 東京都立高校入試 数学 過去問 徹底解説
はじめに
2025年度(令和7年度)東京都立高校入試問題 過去問 数学についての徹底解説記事です。
高校受験の対策、学校の成績や模試の偏差値を上げるためにご活用ください。
※この記事は、林個別指導塾が運営する学習ブログです。
難易度表記
A < B < C < D
A … 入門問題 (この単元を習った時点で解きたい)
B … 基礎問題 (受験までには解けるようにしたい)
C … 発展問題 (解ければ差がつく問題)
D … 難関問題 (かなり難しい問題)
大問1
(1)A (2)A (3)A (4)A (5)A (6)A (7) A (8)B (9)A
(1)から(6)まではシンプルな計算・方程式です。
それぞれについて一言メモを書きました。
最適な途中式を身に付けて、100題出題されても絶対に間違えないようにしましょう!
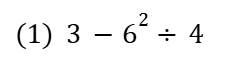
累乗の処理、四則の計算順序に注意!
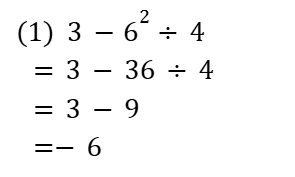
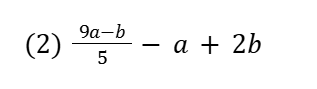
分数が混じった加減の問題は、長分数(ながぶんすう)で処理!

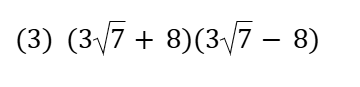
多項式の乗法(展開の処理)は工夫を疑いましょう。

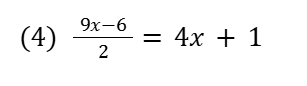
分数の方程式は両辺に掛け算で整数にします。
※分数の計算式とは処理が異なることに注意!!
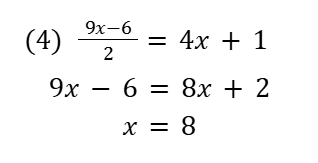
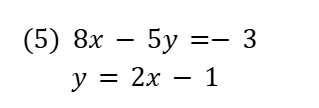
連立方程式は代入法・加減法どちらを使うか決めます。
他の問題と比べて計算間違えが発生しやすいで必ず検算も!
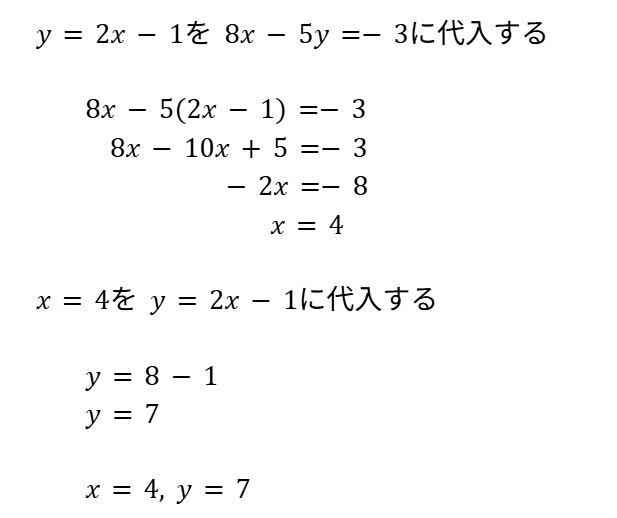
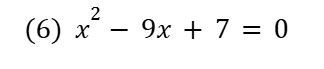
二次方程式は因数分解で解ければ簡単。
無理そうであれば解の公式を使います。
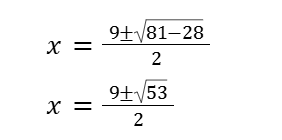
(7)から(9)は問題としては易しいのですが、受験生の準備不足で正答率が下がりがち。
(作図は中1以来ほとんど勉強してない… などの状態の受験生が点数を削られるポイント)
単元ごとの苦手分析&対策がマスト。
※2025年の大問1(7)は例年と傾向が異なるので注意!(大問4で円の図形が出題されるパターンの構成)
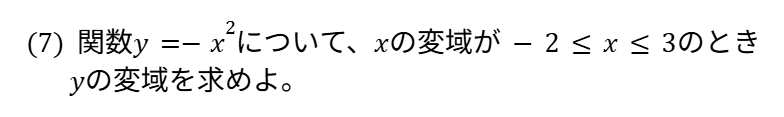
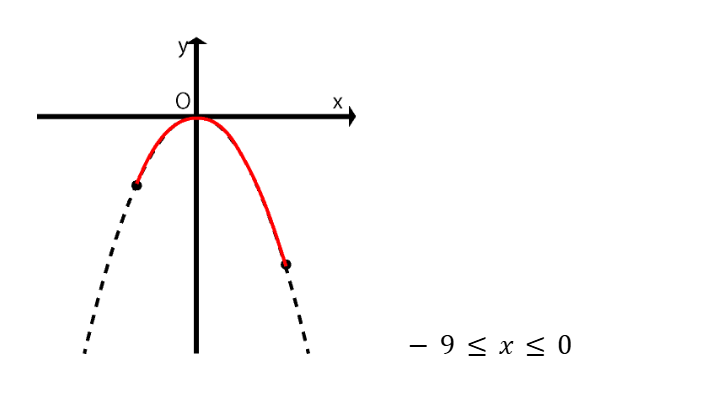
解法の手順
- 点線でグラフを描く
- 変域の両端の点を取る
- 点と点を結ぶ
- グラフをもとに、最大値・最小値を求める

解法の手順
- 問題の設定をつかむ
- 樹形図・マス目の図を書く
- 確率を求める場合は、条件に合うものに〇を付ける
まずは5枚から同時に3枚選ぶ、という問題の設定をつかみます。
同時に選ぶのフレーズは見落とさないように。
イラストを描くと把握しやすいのでおすすめです!
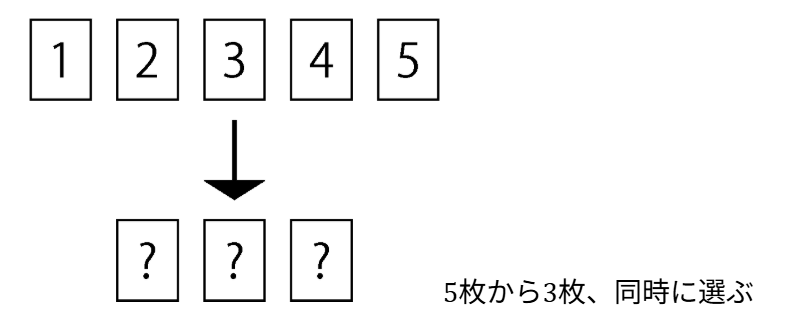
次に、場合の数・確率を数えるための図を作成。
今回は樹形図を書きましょう。
※数字は小さい順に書きます
書きもらし、ダブルカウントがないように注意しましょう。
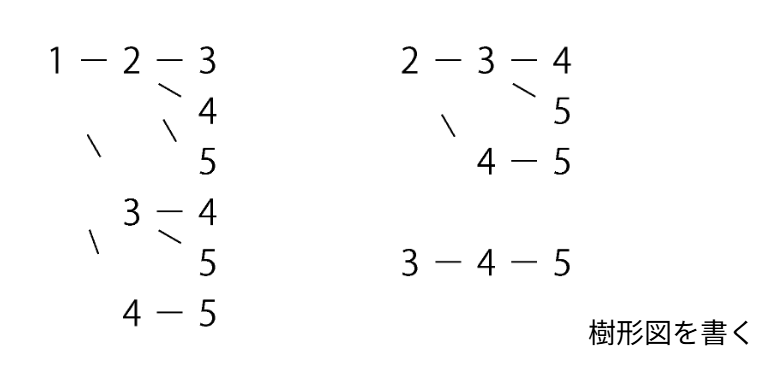
5枚から3枚選ぶパターンの総数が10通りであることが樹形図から分かりました。
次に、今回の題意に沿うパターン数をカウント。
和が10以上の組み合わせに〇をつけます。
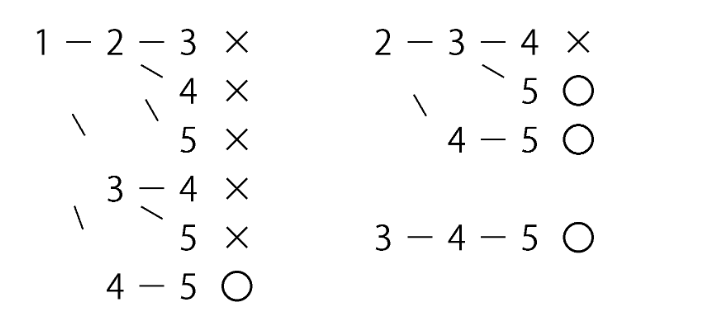
場合の数の総数は10通り、和が10以上の組み合わせは4通り。

必要な処理が多いので難易度Bとしました。

解法の手順
- 作図の根拠となるキーワードを見つける
- それらをもとに作図をする
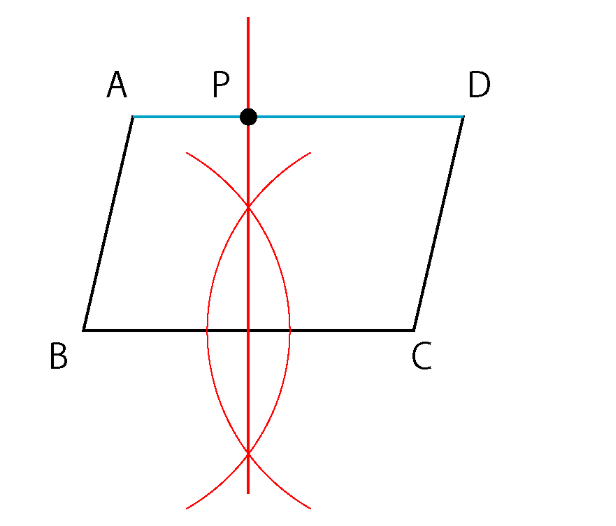
点Pの位置は…
辺AD上 → 作図必要なし
頂点B,頂点Cまでの距離が等しい → 垂直二等分線
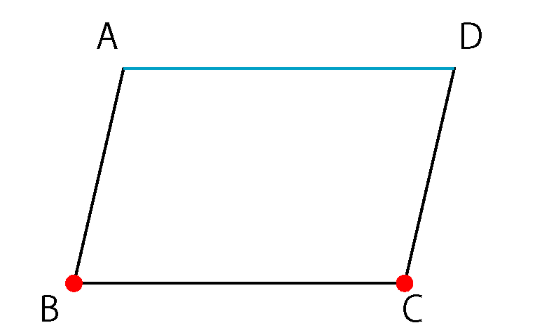
頂点B, C の垂直二等分線を引いて、それとADとの交点を点P とすればクリアです。
大問2
(1)A(別解はB) (2)C
大問2 は規則性の問題。
(2) は証明の記述問題です。

解法を2通り紹介します。
1. 具体的な数値をもとに解く方法
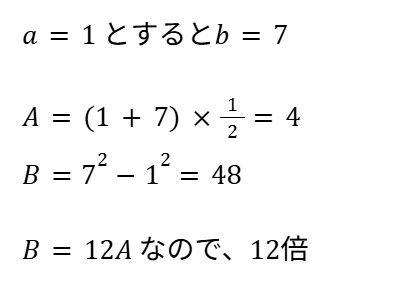
2. 文字を使って解く方法(こちらがオススメ!)

この解法は難易度B で設定しています。
具体的な数値を用いる解法よりも少し難しいですが、可能であればぜひ文字を使って解くことをオススメします。
(2) の証明問題に入る前に、比較的シンプルな設定である(1) を文字式で解いて、性質を見抜いておくことをオススメします。
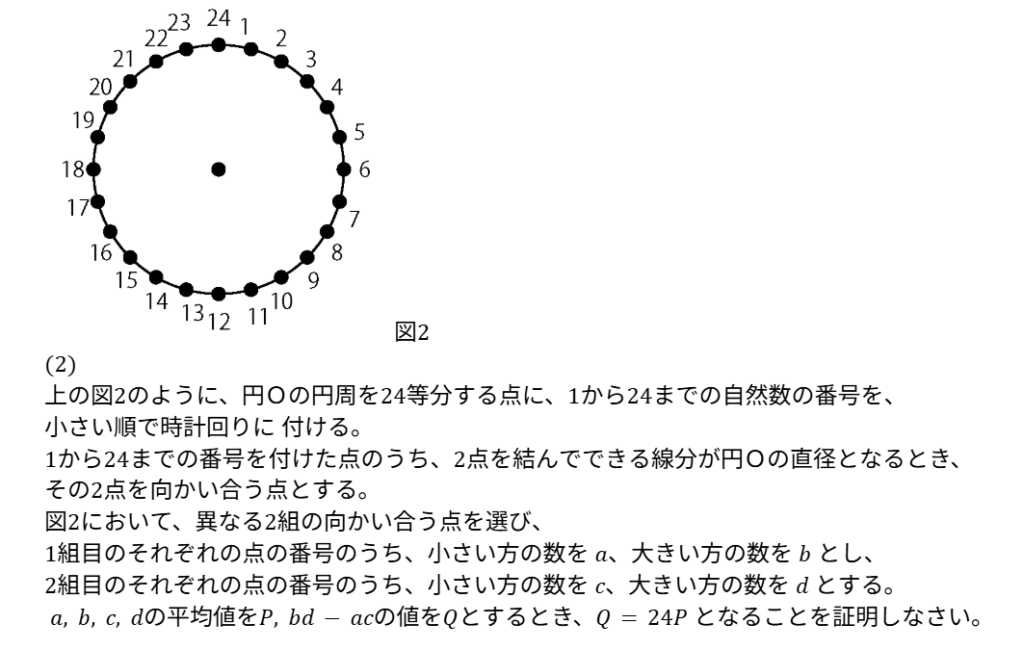
こちらは証明問題。
このパターンは、解法の手順自体は簡単です。
解法の手順
- P を文字を用いて表す
- Q を文字を用いて表す
- Q = 24P を示す
P, Q を文字で表してみると…
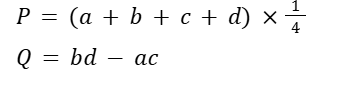
このままでは先に進めないので、a, b, c, d の関係を考えます。
ここで(1) の解法2 が効いてきます。
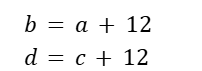
a とb, c とd の関係に着目することで先に進むことができます。
実際の解答は…

証明の過程でa, c の2文字を用いなければならないことから難易度はc としました。
大問3
(1)A (2)A (3)B
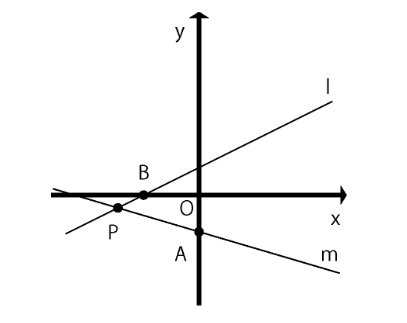

グラフの問題は毎回グラフを書きましょう。
問題文に沿って一つずつ点・線を入れて、その座標や式をメモすることが超重要!


2点の座標から一次関数の式を求める問題。
少し手順が難しいですが、定期テスト・高校入試では超頻出なので必ずできるように。
連立方程式で解くやり方は時間がかかるので、傾きを出してから代入で切片を出す方法をおすすめします。

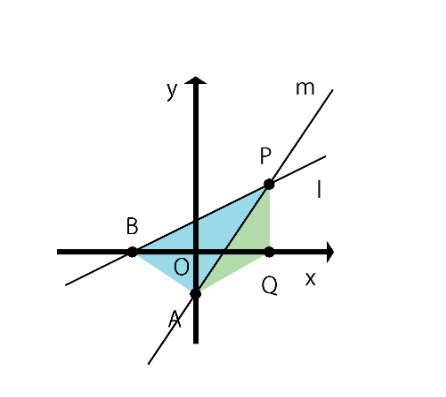


今回の問題は、一つ一つの面積を求めて、立式して解きます。
グラフ問題はこのやり方か、比で解く方法が多いです。
基本的に、比で解く問題の方が難度は高め。
△APB = △AQP × 2 で立式する
△APB … 底辺も高さも分かりにくい三角形 分割 or 等積変形
今回は分割
lとy軸の交点をc として△APB = △CBA + △PCA
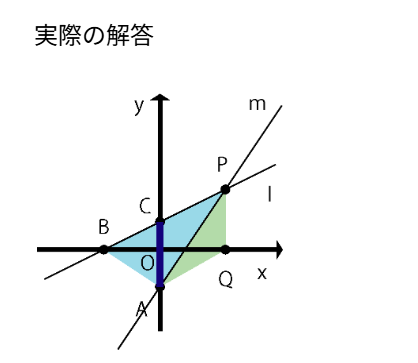
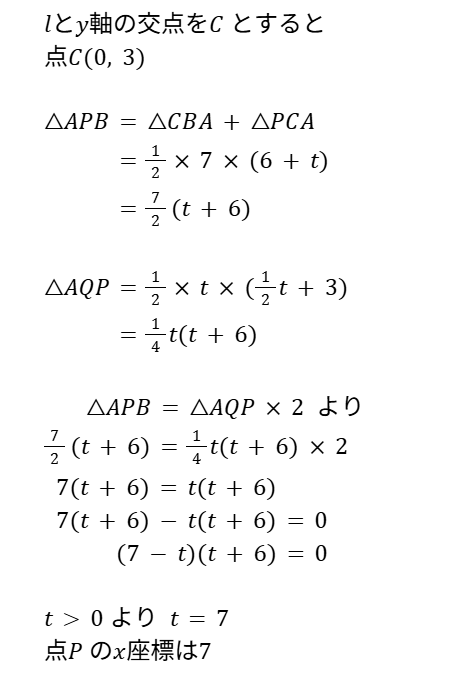
大問4
(1)B (2)①A ②D

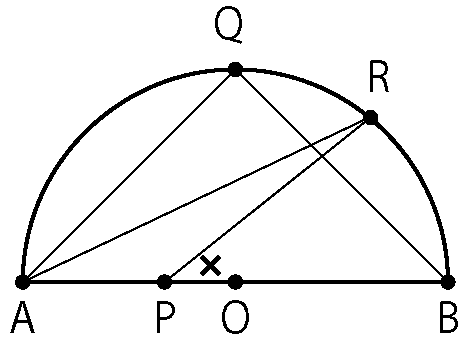
円において中心角・円周角でない角の大きさを求める場合、三角形外角の定理を疑いましょう。
三角形外角の定理:2つの内角の和=残り1つの外角
△APR に着目すると
∠BPR = ∠RAP + ∠ARP
∠RAP と ∠ARP が分かれば解けそうですね。

∠ARP は条件よりa°
∠RAP は少し難しいですね。
△ABQ が直角二等辺三角形であることが見抜ければ求めることができます。

以上より、∠BPR = (a + 25)°

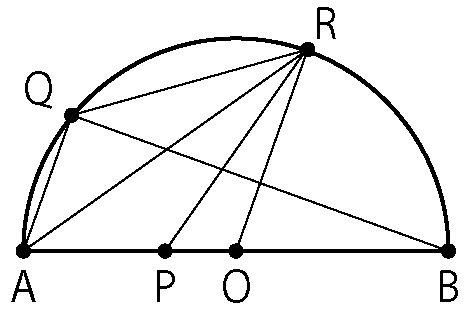
証明問題は図であたりを付けてから記述を始めましょう。
まずは対象の三角形をマークします。
三角形の合同条件を使えるように
- 三組の辺
- 二組の辺とその間の角
- 一組の辺とその両端の角
のいずれかが等しいことをチェックしましょう。
今回は二組の辺とその間の角が等しいことが記述できそうですね。
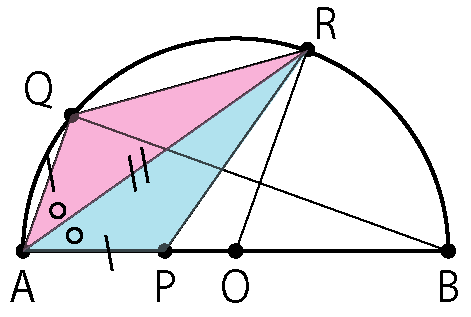


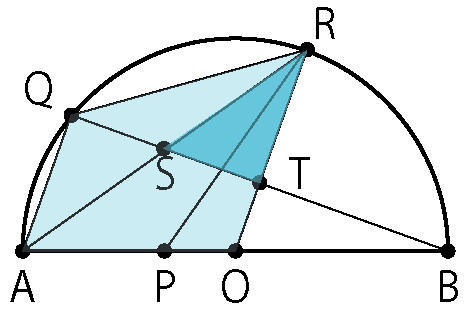
難易度Dレベルの問題!
こちらは林個別指導塾のYouTubeチャンネルでも解説をしています。
考え方は以下の通りです。

まずは辺の比を書き入れます。
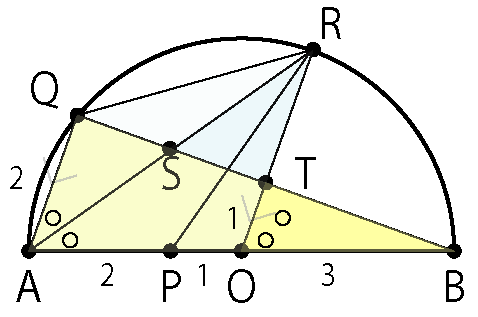
ピラミッドの形を見つけて辺の比を書き足します。
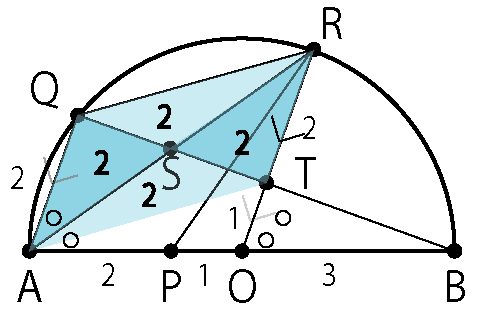
平行四辺形が見えればあと少し!

△AOT の面積比も書き入れてクリアですね。

ピラミッド、平行四辺形、傘の形と見つけるべき形の数が多いので、難易度はDとしました。
大問5
(1)A (2)B

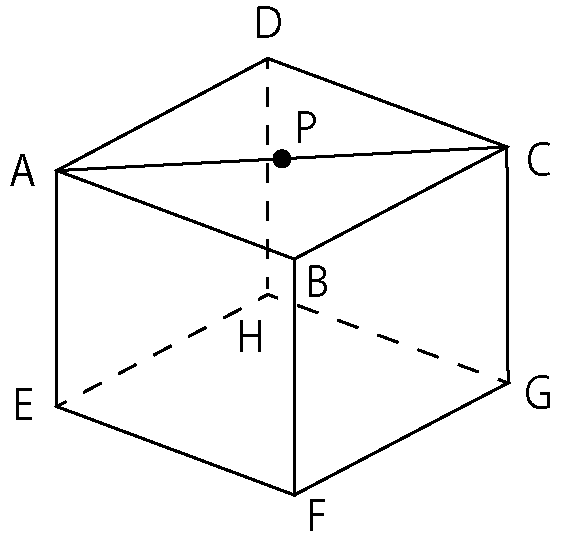
点P が頂点、四角形AEHD が底面の四角錐と見ることができればクリア。
この四角錐の高さは、AB の半分、つまり3 ですね。
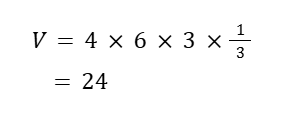
立体図形の演習を積んでいればそれほど難しくないので、難易度はA です。


空間図形のラス問は意外と難しくない(演習を積んでいることが前提)こともよくあります。
今回も実は難易度はそれほど高くないです。
△FPHの底辺FH の長さはすぐにわかります。
FH = 6√2 ですね。
問題なのは高さの方。
これは断面図を取ることでわかります。
HF の中点をQ として、四角形AEGC で断面図を取ります。
この時、PQ の長さが今回求めたい三角形の高さになります。
後は辺の長さを書き入れて、直角三角形をつくって三平方の定理で計算。

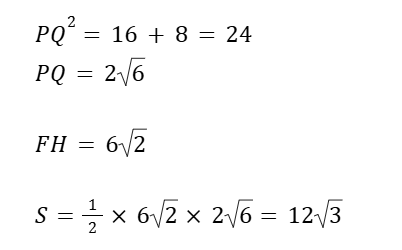
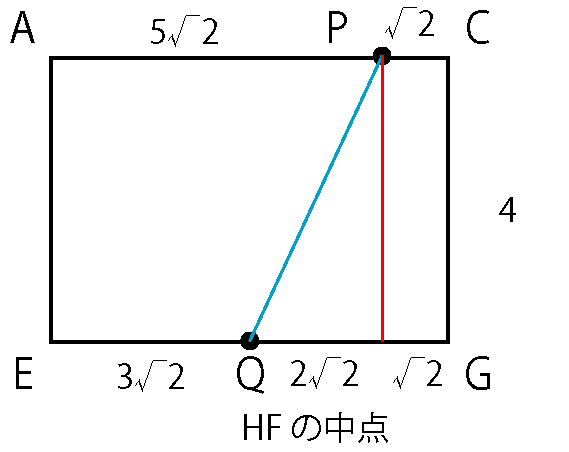
空間図形の演習を重ねていればそれほど意外な流れはなかったので、難易度はB としました。
まとめ
大問4 のラス問は、演習にはよい問題ですが実際に自力で解くのはなかなか難しい。
試験での得点を上げるためには、極端に難しい問題はスルーして、その分他の問題や見直しに時間を割くことをおすすめします。
高校入試の過去問解説を受けたい、受験や定期テストの対策を始めたい方は、ぜひ林個別指導塾にお問い合わせください。
無料の体験授業も行っております。



“【完全版】2025年(令和7年度) 東京都立高校入試 数学 過去問 徹底解説” に対して1件のコメントがあります。
コメントは受け付けていません。