高校数学B「統計的な推測」 第8章|母集団と標本~標本平均の期待値と標準偏差~ やさしく解説

母集団と標本の単元では、新しい語句がたくさん出てきて、なんだか難しく感じますよね。
一つ一つの定義を読んでも、いまいちイメージがわかない…
そんなときは、具体例を交えて考えてみるのが効果的です。
この記事では「全国の高校生の数学の模試の結果」を題材に、母集団と標本、そして標本平均の期待値や標準偏差についてやさしく解説します。
- 「母集団って何?」
- 「標本って何?」
- 「標本平均って何?」
- 「標本平均の期待値や標準偏差の求め方は?」
という疑問を持つ高校生・受験生の方は、ぜひここで基礎を固めて、
共通テスト数学のスコアアップにつなげましょう!
母集団・標本とは?

この記事では「全国の高校生の数学の模試の結果」を題材として解説を進めます。
まずはこの具体例において、母集団・標本が何を表すのかを把握しましょう。
母集団 = 調べたい対象すべての集まり
母集団とは、調べたい対象すべての集まりを指します。
例:「全国の高校3年生全員の数学テストの点数」
このとき
母平均…全国平均点
母標準偏差…点数のばらつき
標本 = 母集団の一部を取り出した集まり
標本とは、母集団の一部を取り出した集まりです。
例:
- 自分のクラス全員の数学テストの点数
- 全国からランダムに100人選んだ高校生の点数
- 全国成績トップ100の高校生の点数
標本の性質はどのように集団を取り出すかによって大きく変わります。
標本平均とは?

標本平均の概要
標本平均とは取り出した標本の平均値です。
具体例…
母集団から5人の生徒を選び、その点数が次のようだったとします。
- 60, 70, 70, 70, 80 → 標本平均 = 70
- 50, 60, 65, 80, 85 → 標本平均 = 68
このように、標本平均は毎回同じ値とは限りません。しかし、完全にランダムというわけではなく、規則性があります。
この章では、標本平均を何度もとった時に
その期待値(大体いくつくらいになるのか)と標準偏差(どの程度ばらつくのか)がどのような値を取るのかを解説します。
標本を無作為に選ぶ重要性
統計的な推測では、標本が無作為(偏りなく)選ばれることが前提です。
偏った集団(同じ学校やトップ生徒だけなど)を選ぶと、標本平均の分布が母集団の性質を正しく表せません。
ちなみに、標本のスコアが母集団と比べて高い場合、「これは偶然か、それとも本当に差があるのか?」と疑問に思います。
この判断に使われるのが検定です(詳細は後の章で解説)。
標本平均の期待値
標本平均の期待値とは、母集団から同じ大きさの標本を何度も抽出したときに、標本平均がどのくらいになるかを表す値です。
具体例
5人ずつ標本を取り、標本平均を何度も計算すると:
70, 69, 74, …
このようにたくさんの標本平均が取れますね。
標本を何度も取り出して平均を取ることで得られる値
これが標本平均の期待値です。
標本平均の標準偏差
標本平均の標準偏差は、標本平均がどの程度ばらつくかを示す値です。
具体例
先ほど取り出した標本平均
70, 69, 74, …
標本平均の期待値と同様に何度も取り出した標本の平均について標準偏差を取ることで得られる値
これが標本標準偏差です。
母集団と標本の関係

母集団と標本には次の重要な関係があります:
- 母平均・母標準偏差が分かる場合
→ 標本平均の期待値と標準偏差を計算できる - 母標準偏差のみ分かる場合
→ 標本平均から母平均を推定できる
この記事では1番目の関係について解説をします。
全国模試の設定
今回は「全国の高校生の数学の模試の結果」を題材にしています。
模試を実施した団体であれば、母集団である生徒一人一人の結果は把握していますよね。
当然そこから母平均や母標準偏差を算出することができます。
~模試の結果~
母平均(μ):60点
母標準偏差(σ):10点
このとき、母集団から100人(n=100)の生徒を無作為に選んだ場合、
標本平均の期待値と標準偏差はどのような値になるのかを見ていきましょう。
標本平均の期待値 = 母平均
標本平均の期待値と母平均の関係です。
標本平均の期待値とは
母集団から同じ大きさの標本を何度も抽出したときに、その平均値はどのくらいになるか
を表す値でしたね。
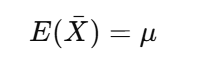
ここで使われている文字の意味は次の通りです。

標本平均の期待値は母平均と等しくなります。
標本の大きさに関係なく公式が成立することも覚えておきましょう。
標本平均の標準偏差 = 母標準偏差 ÷ √標本の大きさ
次は、標本平均の標準偏差と母標準偏差の関係です。
標本平均の標準偏差とは
母集団から同じ大きさの標本を何度も抽出したときに、標本平均がどの程度バラつくか
を表す値でしたね。
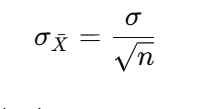
ここで使われている記号の意味は次の通りです。

この式は「標本の数が増えるほど、標本平均のばらつきが小さくなる」ことを表しています。
たくさんの生徒を無作為に選んで平均を取るほど、偶然によるズレが小さくなり、結果が安定していくのです。
標本平均の期待値は母平均をそのまま使えるのに、なぜ標準偏差では√n で割るのか、気になる方も多いですよね。
これについては「標本平均の期待値と標準偏差の公式の導出」コラムで詳しく説明しています。
まとめ
この記事では、「母集団と標本」の基本と、標本平均の期待値・標準偏差の求め方を解説しました。
母集団は全国の高校3年生全員のテスト結果。
標本は、そこからランダムに選んだ100人などのスコアです。
母平均と母標準偏差が分かっている場合
標本平均の期待値 = 母平均
標本平均の標準偏差 = 母標準偏差 ÷ √n
次回は母標準偏差が分かっている場合に、標本平均から母平均を推定する方法を解説します!
標本の平均と標準偏差の確認テスト|この章の理解はバッチリ?
以下のポイントが自力で説明・再現できれば、この章はほぼマスターです!
- 母集団とは何か
- 標本とは何か
- 標本平均の期待値の求め方
- 標本平均の標準偏差の求め方
「ちょっと怪しいかも…」と思った箇所があれば、上に戻って再チェックしてみましょう!
◀ 第7章|正規分布~二項分布の近似~
▶ 第9章|母集団と標本~母平均の推定~
▶︎高校数学B「統計的な推測」シリーズ目録・過去問解説のまとめはこちら!
共通テスト・大学入試に向けて勉強を始めたい方は、林個別指導中にお問い合わせください。
無料のオンライン体験授業も用意しております!



“高校数学B「統計的な推測」 第8章|母集団と標本~標本平均の期待値と標準偏差~ やさしく解説” に対して6件のコメントがあります。
コメントは受け付けていません。