高校数学B「統計的な推測」 第9章｜母集団と標本～母平均の推定～ やさしく解説

母集団と標本の単元では、新しい語句がたくさん出てきて、なんだか難しく感じますよね。

一つ一つの定義を読んでも、いまいちイメージがわかない…

そんなときは、具体例を交えて考えてみるのが効果的です。

この記事では「果樹園の収穫」を題材に、母集団と標本、そして母平均の推定についてやさしく解説します。

という疑問を持つ高校生・受験生の方は、ぜひここで基礎を固めて、
共通テスト数学のスコアアップにつなげましょう！

母集団・標本・標本平均とは？（復習）

この記事では「果樹園の収穫」を題材として解説を進めます。

まずはこの具体例において、母集団・標本が何を表すのかを把握しましょう。

母集団 = 調べたい対象すべての集まり

母集団とは、調べたい対象すべての集まりを指します。

今回は「果樹園にあるすべてのリンゴ」を母集団とします。

このとき
母平均…リンゴの平均重量
母標準偏差…重さのばらつき

標本 = 母集団の一部を取り出した集まり

標本とは、母集団の一部を取り出した集まりです。

例えば、果樹園から10個のリンゴだけを取り出して重さを測る──この10個が標本です。

標本の選び方にはさまざまな方法が考えられます。

しかし標本と母集団の関係が知りたい場合は、
標本を無作為に選ぶことが重要です。

この記事では、
標本を選ぶ = 「収穫したリンゴ全体から無作為に10個のリンゴを選ぶ」
として話を進めます。

標本平均 = 取り出した標本の平均値

標本平均とは取り出した標本の平均値です。

この記事では、
標本平均 = 「無作為に選んだ10個のリンゴの平均重量」
とします。

標本平均は測定するたびに数値が変わり得ることに注意してください。

毎回選んでくるリンゴは別のものなので、当然その重量も異なります。
それらの平均値（標本平均）は、標本を選び直すたびに数値が変わる可能性がありますよね。

標本平均は毎回同じとは限りませんが、
ある程度の規則性は存在します。

標本平均の期待値と標準偏差については「統計的な推測シリーズ第８章」で詳しく解説しています。

是非チェックしてください。

高校数学B「統計的な推測」 第8章｜母集団と標本～標本平均の期待値と標準偏差～ やさしく解説

この標本平均と母平均の関係を考えることが、この記事のメインテーマです。

標本平均から母平均を推定する

果樹園のリンゴすべての平均重量を求めるには…

母平均である「果樹園のすべてのリンゴの平均重量」を実測で求めることは現実的ではありません。

一つ一つのリンゴの重さをはかるには莫大なコストと時間がかかります。

このように母平均を測定することができないときに役立つのが
母平均と標本平均の関係です。

標本平均の期待値 = 母平均

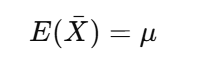
標本平均の平均（＝期待値）は、母平均と一致します。

つまり「標本平均は母平均の“良い推定量”である」と言えます。

母平均はわからずとも、標本平均は簡単に測定できます。

今回の具体例では、リンゴを無作為に10個用意してそれらの平均重量を求める。
これだけで標本平均を求めることができます。

この標本平均を活用することで、
実際にすべてのリンゴの重量を調べずとも母平均を推定することができます。

これから二種類の推定方法を解説します。

母平均を推定する二つの方法

1. 点推定で母平均を推定する

例えば、標本平均を１セット調べた時、
リンゴ10個の重さが285gだったとします。

点推定では、この標本平均（285g）をそのまま母平均と推定します。

この方法であれば簡単に母平均を推定することができますね。

点推定のデメリット

ただし、点推定はお手軽な反面デメリットも多く存在します。

まず、当然ながらこの点推定は母平均からずれる可能性があります。

さらに、このずれ（誤差）がどれくらいあるのかもわからない。

この推定された母平均をどの程度信頼してよいのかが不明ですよね。

これらの問題点を解決するために、二つ目の推定方法あります。

2. 区間推定で母平均を推定する

点推定では、標本平均そのものを母平均とみなしました。

しかし、標本平均はあくまで「たまたま選ばれた標本の平均」です。

そのため、母平均より大きめになることもあれば、小さめになることもあります。

そこで次に登場するのが 区間推定 です。

区間推定とは、
「母平均は、この範囲のどこかにあるはずだ」と 幅（区間）をつけて推定する方法 です。

これによって、
点推定の弱点だった「誤差がどれくらいあるかわからない」という問題を補うことができます。

区間推定と信頼区間

区間推定を考えるうえで、欠かせないのが 信頼区間 という考え方です。

信頼区間は「信頼度○○%の信頼区間」のように、
数値で補足されます。

「信頼度○○%の信頼区間」とは
同じ条件で何度も区間推定を行ったとき、
そのうち○○%の区間が、母平均（固定値）を含むように作られている

もう少しかみ砕いて説明すると
同じ手続きで区間を100回作れば、そのうち約○○回は母平均を含むように設計されている

という意味です。

ここで注意したいのが、
母平均がいろいろな値を取り、○○%の確率で区間に入るという考え方は誤り
であることです。

母平均は「1つに定まった固定の値」です。
ゆらぐのは母平均ではなく、標本平均 → 区間のほうです。

高校数学Bの統計では、信頼度95%の信頼区間 を推定する場合がもっとも多いので、
この記事でもこの設定で説明していきます。

区間推定の公式

母平均の区間推定は、
標本平均とそのばらつき（標本平均の標準偏差）を考えることで求められます。

高校数学Bでは、母集団が正規分布に従い、母標準偏差 σ が分かっている場合、
母平均 μ の信頼度95%の信頼区間は次の式で求めます。

$\bar{X}−1.96\dfrac{σ}{\sqrt{n}}≤μ≤\bar{X}+1.96\dfrac{σ}{\sqrt{n}}$

（1.96 は正規分布の性質から出てくる定数です。）

この公式を用いて、実際に果樹園のリンゴの母平均を区間推定してみましょう！

例題：果樹園のリンゴの平均重量は？

この記事で具体例として用いている「果樹園のリンゴの平均重量」について、
実際に区間推定を行いましょう。

問題文から

$\bar{X}=285, σ=20, n=10, 信頼度は95\%$

これらの数値が読み取れます。

これらを公式に代入すると…

$\bar{X}−1.96\dfrac{σ}{\sqrt{n}}≤μ≤\bar{X}+1.96\dfrac{σ}{\sqrt{n}}$

$285−1.96\times\dfrac{20}{\sqrt{10}}≤μ≤285+1.96\times\dfrac{20}{\sqrt{10}}$

$285−1.96\times2\sqrt{10}≤μ≤285+1.96\times2\sqrt{10}$

$285−12.4≤μ≤285+12.4$

$272.6≤μ≤297.4$

リンゴの平均重量に対する信頼度95%の信頼区間は
272.6g 以上 297.4g である。

まとめ

母平均が測定できない場合は、標本平均を用いて推定することができます。

点推定と区間推定のうち、高校数学B 統計的な推測では区間推定がよく出題されます。

信頼区間の考え方、区間推定の公式とその活用法をしっかりと確認して
共通テストや定期試験に備えましょう！

母平均の推定の確認テスト｜この章の理解はバッチリ？

以下のポイントが自力で説明・再現できれば、この章はほぼマスターです！

• 母集団とは何か
• 標本とは何か
• 点推定とは何か
• 区間推定と何か
• 信頼区間とは何か
• 信頼区間の求め方

「ちょっと怪しいかも…」と思った箇所があれば、上に戻って再チェックしてみましょう！

---

◀ 第８章｜母集団と標本～標本平均の期待値と標準偏差～
▶ 第10章｜仮説検定の考え方

▶︎高校数学B「統計的な推測」シリーズ目録・過去問解説のまとめはこちら！

---

共通テスト・大学入試に向けて勉強を始めたい方は、林個別指導中にお問い合わせください。

無料のオンライン体験授業も用意しております！

▶︎ [公式LINEに登録する]
▶︎ [お問い合わせフォームへ]