確率変数の変換 Y=aX+b ｜期待値・分散が分からなくなるポイントは「何をX と置くか」

箱の中に赤玉と白玉が入っていて、
いくつか取り出した結果によって「賞金」が決まる。

共通テストや定期テストでは、このように
設定が少し複雑な期待値・分散の問題がよく出てきます。

このような複雑な設定の問題に取り組む際に、
賞金を直接、確率変数X でとっていませんか？

実はこのタイプの問題ではその取り方をすると、
期待値や分散の計算が一気に面倒になります。

この問題は「賞金以外のあるもの」を確率変数X と取ることで、
計算の手間を格段に減らすことができます。

その考え方が「確率変数の変換 Y = aX + b」です！

という疑問を持つ高校生・受験生の方は、ぜひここで基礎を固めて、
共通テスト数学の得点アップにつなげましょう！

確率変数X に対する期待値・分散・標準偏差の公式（復習）

今回のメインテーマに入る前に、
確率変数X に対する期待値・分散・標準偏差の公式を確認しておきましょう。

期待値の公式

分散の公式

確率変数X の期待値・分散・標準偏差の公式の使い方が心配な方向けに、
「第2章｜期待値と分散・標準偏差」で詳しく解説をしています。

高校数学B「統計的な推測」 第2章｜確率変数の期待値・分散・標準偏差をやさしく解説

確率変数X に対する基本的な公式が大丈夫な方は、
今回のメインである「確率変数の変換」へ進みましょう！

確率変数の変換とは？ （Y = aX + b）

確率変数の変換とは、
元の確率変数 X の値を、別の形に置き換えて新しい確率変数 Y を作ることをいいます。

その中でも、最もよく使われるのが
線形変換（Y = aX + b） と呼ばれる変換です。

なぜ変換を行うの？

「確率変数ってわざわざ変換しないといけないの？」

新しい手順や公式を覚えることを面倒に感じるかもしれませんが、
確率変数を変換するのにはきちんとした理由があります。

これら２つが特に大きな理由です！

確率変数の変換をする・しないでは、
計算の複雑さと設定変更への柔軟さに大きな差があります。

「確率変数の変換をする・しない」の２パターンのアプローチの比較検証記事で、
確率変数の変換のメリットを体感してください！

高校数学B「統計的な推測」確率変数の変換が必要な理由｜やさしく解説

この章では、
確率変数の変換方法とその数値の算出法にフォーカスします。

次は変換の公式を解説します。

確率変数の変換｜期待値・分散を求める公式

確率変数Xに対して、Y = aX + b と変換したとき、Y の期待値と分散は以下のように求められます。

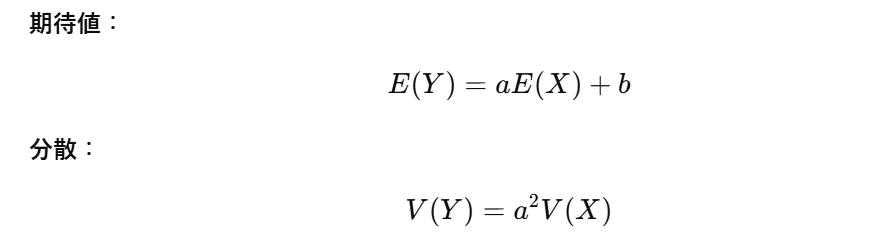
このように、
X の期待値や分散がわかっていれば、Y の期待値・分散もすぐに計算できます。

この変換公式がどのように導かれるのか気になる方は、
以下の記事で詳しく解説していますのでぜひご覧ください。

高校数学B「統計的な推測」 線形変換の期待値・分散の変換公式の証明 やさしく解説

確率変数の変換のメリットと公式まではわかったけど、
実際の問題演習で何を確率変数でとればよいか分からない…

このような悩みを持つ方は、
次の「確率変数X ・Y の置き方」で解決しましょう！

確率変数の変換｜確率変数X・Y の置き方

確率変数の変換が便利なのはわかったけど、
実際、確率変数X・Y はどのように置けばいいのだろう…

その悩みもここで解決しましょう！

求めたいものが何によって決まっているか考える

冒頭の例題です。

確率変数X がとる値と、
確率変数Y の表し方について考えましょう。

ここで問われているのは「賞金について」ですね。
なので確率変数Y は賞金です。

次に考えるのは、その賞金は何によって決まっているのか…

「赤玉1つにつき100円もらい、白玉1つにつき120円支払う」

そうです、賞金は引いた球の色によって決まっています。
これを確率変数X で置きましょう。

この場合は例えば、
「引いた赤玉の個数」を確率変数X と置くのが一つの正解です。

最後に Y = aX + b の係数を決定します。

引いた赤玉の個数がX ならば、引いた白玉の個数は２ – X

赤玉1つにつき100円もらい、白玉1つにつき120円支払うので

$Y=100 \times X -120(2-X)$
$=220X -240$

これでクリアです！

---

もう１題、練習をしてみましょう。

こちらも、確率変数X がとる値と、
確率変数Y の表し方について考えましょう。

問われているのは走る時間です。

確率変数Y 「走る時間」

走る時間が決まる要素は「コインの表裏」ですね。

この場合は「表のコインの枚数をX 」とおくと良いです。

表のコインの枚数がX なら、裏のコインは ３ – X 枚。

表の枚数１枚につき10分、裏の枚数１枚につき5分走るから

$Y=10X +5(3-X)$
$=5X+15$

何を確率変数Ｘ で置けばよいか迷ったときは
求めたいものが何によって決まっているか考えましょう。

次は例題で、実際に期待値・分散まで求めます！

例題｜確率変数の変換を使ってみよう

Y = aX + b の変換と期待値・分散について実際に具体例で求めてみましょう！

ここから先は、確率変数X について期待値・分散を求めるスキルが必須です。

確率変数X についての期待値・分散の計算方法が不安な方は、
第2章「期待値と分散・標準偏差」で復習をしましょう。

高校数学B「統計的な推測」 第2章｜確率変数の期待値・分散・標準偏差をやさしく解説

例題：賞金の問題

この記事で繰り返し触れているこの問題について、
期待値・分散まで求めましょう。

確率変数X・Y を決める

問われているのは賞金ですが、
それを決めているのは「引いた球の色」です

確率変数X … 取り出した２個のうち赤玉の数
確率変数Y … 賞金

このように置きます。

賞金（確率変数Y）ついてY = aX + b に変換する

賞金を aX + b の形 に変換します。

赤玉が X 個 出たとすると、残りの 白玉は（2 − X）個

赤玉 1 個につき +100円、白玉 1 個につき −120円

よって、

$Y=100X -120(2-X)$

$Y=220X -240$

このように変換されます。

確率変数X（赤玉の個数） の期待値・分散を求める

ここはスムーズに突破しましょう！

確率分布を表にまとめます。

X	$0$	$1$	$2$	計
P(X)	$\dfrac{1}{15}$	$\dfrac{7}{15}$	$\dfrac{7}{15}$	$1$

この表をもとに計算を進めるのですが…

今回のようにE[X], E[X²] まで求めるような場面では、Xを縦にとった表でまとめてもOKです。

X（赤玉の数）	確率P(X)	X × P(X)	X² × P(X)
$0$	$\dfrac{1}{15}$	$0$	$0$
$1$	$\dfrac{7}{15}$	$\dfrac{7}{15}$	$\dfrac{7}{15}$
$2$	$\dfrac{7}{15}$	$\dfrac{14}{15}$	$\dfrac{28}{15}$
計	$1$	$\dfrac{7}{5}$	$\dfrac{7}{3}$

E[X], E[X²] について計算

$E[X]=\frac{1}{15}\times(7+14)$
$=\frac{7}{5}$

$E[X^2]=\frac{1}{15}\times(7+28)$
$=\frac{7}{3}$

これらをもとに、期待値・分散を求めましょう。

期待値：

$E[X]=\frac{7}{5}$

$V[X]=E[X^2] – (E[X])^2$

$=\frac{7}{3}-(\frac{7}{5})^2$

$=\frac{28}{75}$

これで「確率変数X 」についての計算はクリア。

これをもとに「確率変数Y 」について考えます。

賞金（確率変数Y）について期待値・分散を求める

$Y = 220X – 240$ の期待値・分散を公式で求めます。

期待値：

$E[Y]=220\times E[X]-240$
$=220\times \frac{7}{5}-240$
$=68$

分散：

$V[Y]=220^2\times V[X]$
$=48400\times \frac{28}{75}$
$≒45173.33$

これでクリア！

例題：時間の問題

こちらも確率変数の置き方を練習した問題です。

走る時間の期待値・分散まで算出してみましょう。

確率変数X・Y を決める

問われているのは走る時間ですが、
それを決めている要素は「表のコインの枚数」です。

確率変数X … 表のコインの枚数
確率変数Y … 走る時間

このように設定しましょう。

賞金（確率変数Y）ついてY = aX + b に変換する

走る時間を aX + b の形 に変換します。

$Y=10X +5(3-X)$
$Y=5X +15$

このように変換されます。

確率変数X（表のコインの枚数） の期待値・分散を求める

ここはスムーズに突破しましょう！

確率分布を表にまとめます。

Xを縦にとった表でまとめます。

X（表のコインの枚数）	確率P(X)	X × P(X)	X² × P(X)
$0$	$\dfrac{1}{8}$	$0$	$0$
$1$	$\dfrac{3}{8}$	$\dfrac{3}{8}$	$\dfrac{3}{8}$
$2$	$\dfrac{3}{8}$	$\dfrac{6}{8}$	$\dfrac{12}{8}$
3	$\dfrac{1}{8}$	$\dfrac{3}{8}$	$\dfrac{9}{8}$
計	$1$	$\dfrac{3}{2}$	3

E[X], E[X²] について計算

$E[X]=\frac{1}{8}\times(3+6+3)$
$=\frac{3}{2}$

$E[X^2]=\frac{1}{8}\times(3+12+9)$
$=3$

これらをもとに、期待値・分散を求めましょう。

期待値：

$E[X]=\frac{3}{2}$

$V[X]=E[X^2] – (E[X])^2$

$=3-(\frac{3}{2})^2$

$=\frac{3}{4}$

これで「確率変数X 」についての計算はクリア。

これをもとに「確率変数Y 」について考えます。

賞金（確率変数Y）について期待値・分散を求める

$Y=5X +15$ の期待値・分散を公式で求めます。

期待値：

$E[Y]=5\times E[X]+15$

$=5\times \frac{3}{2}+15$

$=\frac{45}{2}$

分散：

$V[Y]=5^2\times V[X]$

$=25\times \frac{3}{4}$

$=18.75$

これでクリア！

解き方の確認

どちらの例題もこの手順で解きました。

確率変数X の計算に入る前にX・Y で表すものを決めておくと、
思わぬミスを防ぐことができます。

演習

今回は白玉の支払額の取りうる最大値。

例題とは問われていることが違いますが、それでも解法の手順はほぼ同じです。

確率変数の宣言（例題１より）

確率変数X … 取り出した２個のうち赤玉の数
確率変数Y … 賞金

賞金Y を aX + b に変換する

$Y=100X -a(2-X)$

よって

$Y=(100+a)X -2a$

確率変数X の期待値・分散（例題１より）

$E[X]=\frac{7}{5}$

$V[X]=\frac{28}{75}$

確率変数Yについて期待値を求める

$Y=(100+a)X -2a$ より

$E[Y]=(100+a) \times E[X] -2a$

$E[Y]=(100+a) \times \frac{7}{5} -2a$

$E[Y]=\frac{1}{5} (700-3a)$

公式を用いてYの期待値を算出。

期待値が正になる条件を考える

賞金の期待値がプラスになるには
$E[Y]>0$ となればよいので

$\frac{1}{5} (700-3a)>0$

$3a<700$

$a<233.33…$

つまり白玉の支払額として設定できるの最大値は233円
ということになります！

賞金を最初から Y として直接処理しようとすると、
Y の取りうる値が文字式だらけになり、先に進むことがかなり厳しくなります。

しかし、このように赤玉の数を X として処理 → 確率変数の変換 → 賞金の処理の順でこなすことで
とてもスマートに解くことができます。

この問題も線形変換の便利さがよくわかる一例ですね。

まとめ

Y = aX + b の形で確率変数を変換すると、
期待値・分散をスマートに求めることができます。

これは変換法を新たに覚えるに値する価値です。

問題演習を通して、
何を確率変数X として確率変数Y を表せばよいのかを学びましょう。

次に学ぶのは、
「確率分布をまとめる」を経由せずに期待値・分散を求める方法。

「第４章｜二項分布・ベルヌーイ分布」でさらなる処理の短縮を身に付けましょう！

aX + b の変換と期待値・分散の変化の確認テスト｜この章の理解はバッチリ？

以下のポイントが自力で説明・再現できれば、この章はほぼマスターです！

• 確率変数X に対する期待値・分散の公式
• なぜaX + b の形へ変換（線形変換）するのか
• 確率変数Y( = aX + b)に対する期待値・分散の公式
• 確率変数Y( = aX + b)に対する期待値・分散の公式の証明

「ちょっと怪しいかも…」と思った箇所があれば、上に戻って再チェックしてみましょう！

---

◀第２章｜期待値と分散・標準偏差
▶第４章｜二項分布・ベルヌーイ分布

▶︎高校数学B「統計的な推測」シリーズ目録・過去問解説のまとめはこちら！

---

共通テストに不安がある方は、お気軽にご連絡ください。

無料のオンライン学習相談・体験授業をご用意しています！

▶︎ [公式LINEに登録する]
▶︎ [お問い合わせフォームへ]