東京都 公立高校入試 数学 大問4(平面図形)|図形が苦手でも点を取る考え方

東京都立高校入試の数学で、
「対策で結果に、最も差が出る」
それが大問4の平面図形です。
- 補助線が思いつかない
- 証明になると手が止まる
- 最後の問題は、見た瞬間に諦めてしまう
多くの受験生が、各小問ごとに悩みを持っています。
ですが実は、
大問4は対策法がはっきりしている単元です。
点が取れない原因の多くは、
- 図を正しく書けていない
- 文章と図を結びつけて読めていない
- 「どこまで取れば十分か」が分かっていない
このあたりにあります。
大問4は、
- 取るべき問題
- 割り切ってよい問題
がはっきりしている大問です。
つまり、戦い方を間違えなければ、得点は安定します。
この記事では、
- 大問4(平面図形)の出題構成
- 各小問の役割と狙い
- どこまでできれば合格ラインに届くのか
- 図形が苦手な人が最初に意識すべき考え方
を、順番に整理していきます。
「平面図形が苦手で不安」
という方は、まずここで考え方の土台を整えてください。
東京都 公立高校入試 数学 大問4 概要

東京都都立高校入試の数学 大問4は、平面図形の問題です。
- 多角形(四角形)
- 円
これらのうちどちらかが問題が毎年出題されます。
※基本的には多角形が出題されます。
最近では令和7年度、3年度に円が出題されました。
続いて、小問の構成について解説をします。
(1) 文字式で角度を答える問題 …5点
(2)① 合同・相似の証明 …7点
(2)② 辺や面積の比・大きさを答える問題 …5点
大問4では小問が3題出題されます。
(1)と(2)①が必ず解きたい問題、
(2)②はほとんどの受験生にとってスルー推奨の問題です。
各年度で出題された図形

各年度でどのような図形が出題されたのか確認しておきましょう。
- 2025年度 … 円(半円)
- 2024年度 … 四角形(長方形)
- 2023年度 … 四角形(台形)
- 2022年度 … 四角形(ひし形)
基本的には四角形についてしっかりと対策を行って、
仮に円が出題されても基本問題は解ける状態にしましょう。
学校のカリキュラム上、円の問題は演習不足になりがちです。
最低でも過去問2回分は、円の問題を解いておくことをおすすめします。
東京都 公立高校入試 数学 大問4 ラス問は飛ばす?

都立高校入試 数学の中で最も難しい問題
それが大問4の最後の小問です。
2020年度から2025年度の正答率は
平均3.5%( 0.5~6.6%)
つまり、問題が簡単だとしても正答率6%程度ということです。
本番の目標点数によって戦略を決めましょう。
本番の目標点数が83点未満の場合
大問4のラス問は本当に難度が高いので、
受験の戦略上スルーする、が基本的な作戦です。
過去問演習の際にもこの問題には触れずに、その分他の問題に時間を割くことが
かなり有効な取り組み方です。
受験までの準備時間が限られている入試の戦略上、スルー推奨の問題です。
本番の目標点数が83点以上の場合
大問4のラス問を解くためには、正直言うと学校の授業やテストだけでは足りないです。
平面図形の問題が収録された問題集を手に入れて、演習を多く積みましょう。
一つ一つの問題がかなり難しいですがそれらをしっかりと吸収して、
入試レベルの問題に太刀打ちできる力を身に付けましょう。
東京都 公立高校入試 数学 大問4 各小問の対策

大問4 平面図形に取り組むために非常に重要なポイントを確認してから、
各小問の対策についてチェックをしましょう。
★文章に沿って自分で図を書く
図形問題で最も重要なことは「文章に沿って自分で図を書く」ということ。
これは題材が多角形でも円でも同様です。
大問5で問われる空間図形もやはり同様です。
文章に沿って図を書き進めながら、その都度重要な関係を書き込み、場合のよっては図を抜き出していく。
ある三角形の二組の辺が等しいことが分かったら、底角にも同じ印をつける。
重なった図形の合同・相似が問われる場合は、必要な図を抜き出す。
このように、設問に振り回されることなく、重要な関係を把握する。
このことを前提に読み進めてください。
問1 文字式で角度を答える問題
問1は、文字式で角度を答える問題です。
一か所の角度が文字式で与えられていて、別の角度についてその文字式を用いて表す問題です。

例:2025年度 後期の問題
値が分かりそうな角度をやみくもに求めていくのではなく、
どの角度が分かれば答えに近づくのかを考えて解くことをおすすめします。

平行線の錯角は等しいので、∠DAP = ∠BPA
三角形の内角の和は180°なので、a + 50 + ∠BPA = 180
∠BPA = 130 – a より
∠DAP は (130 – a)°
今回の例題では、∠BPA が分かれば答えを求めることができますね。
大問4は問1はどうしても答えが思い浮かばないこともあります。
その場合は、問1が解けなくとも問2(1)へ進みましょう。
問2① 合同・相似の証明
問2は合同・相似を記述で証明する問題です。
配点は7点。
ここで安定して得点できる(難問が出題されても部分点は確保する)ことが、
高校入試の戦略上、非常に重要です。

例:2025年度 後期の問題
まずは、自分で図を書いて重要な関係を見抜いて解きましょう。
証明したい図形どうしが重なっている場合は、きちんと図を抜き出して考えましょう。
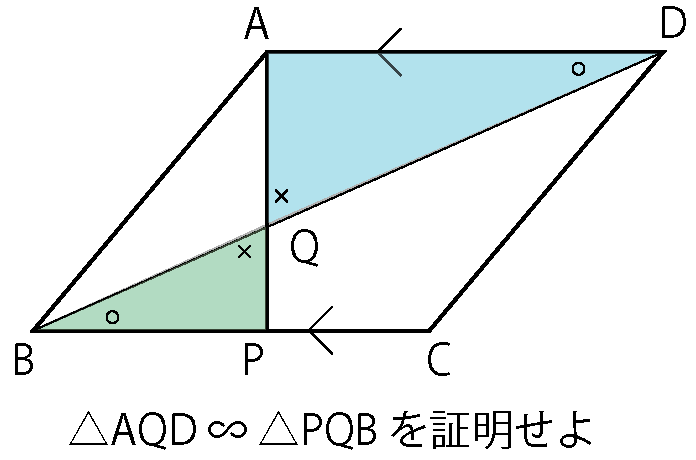
平行線の錯角
対頂角
ふたつの角がそれぞれ等しいことを見抜いて、図に印をつけます。
解答に必要な関係を見抜くことができたら、今度は記述のトレーニング。
証明の記述は、教科書レベルの簡単な問題からしっかりトレーニングしましょう。
問2② 辺や面積の比・大きさを答える問題
※この問題は本番で80点以上得点したい人向けのものです。
まずは問1、問2①を安定させたい人は飛ばして大丈夫です。
問2②は辺や面積の比・大きさを答える問題です。
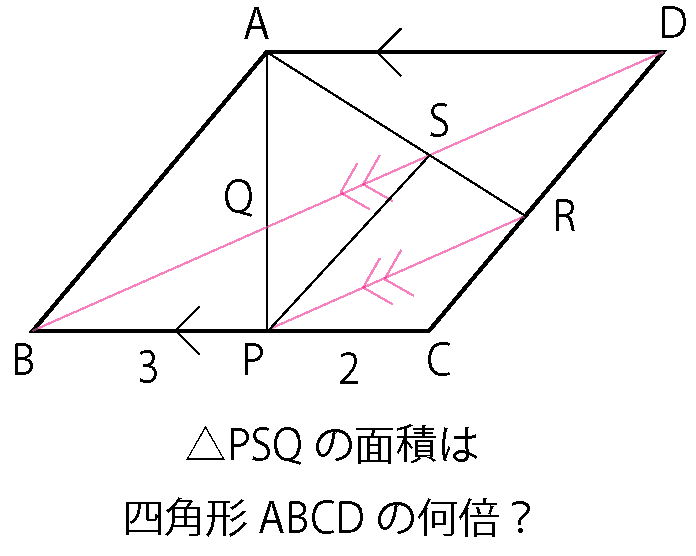
例:2025年度 後期の問題
今までの問題と比べて明らかに難しいですね。
都立高校入試 数学の中で最も難しい問題がこの小問です。
今回の例題は…

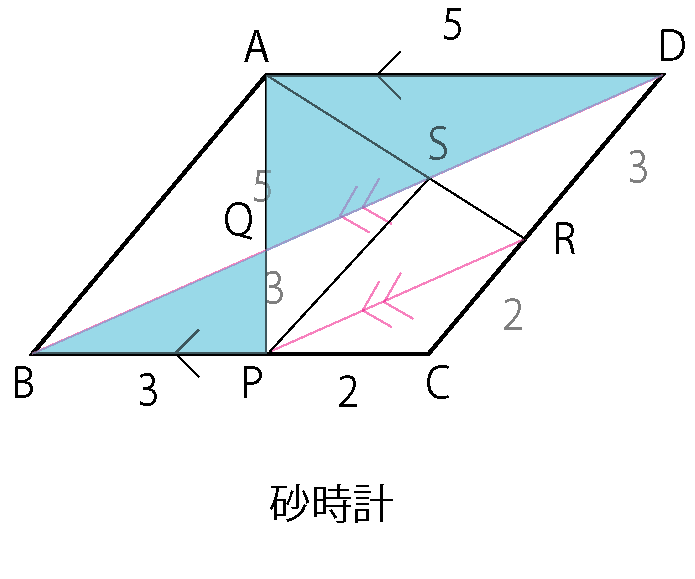
ピラミッド・砂時計を駆使して、まずAQ : QP =5 : 3 を見抜く。

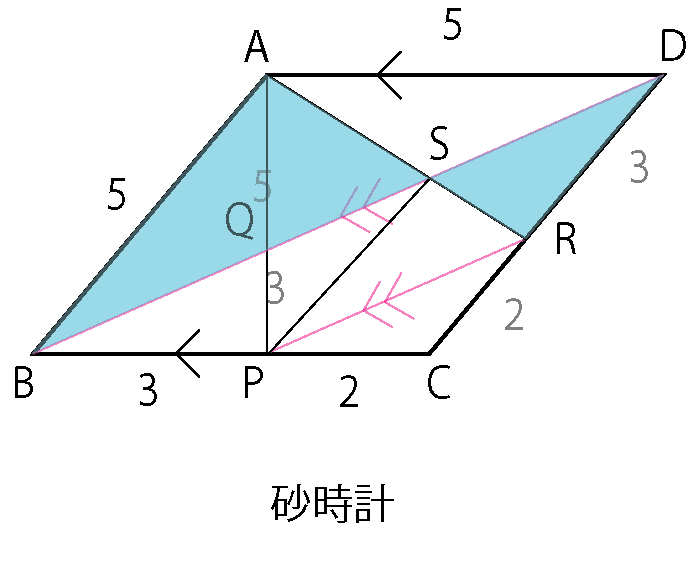
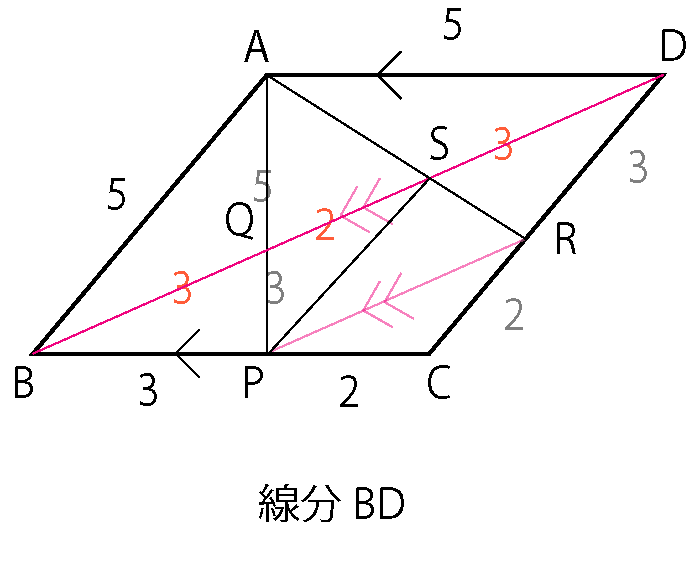
砂時計ふたつを駆使して線分BD について、BQ : QS : SD = 3 : 2 : 3 を見抜く。
最後に仕上げ。
△ABD = △PSQ × 5/3 × 8/2 = △PSQ × 20/3
四角形ABCD = △ABD × 2 = △PSQ × 40/3
よって△PSQ は、四角形ABCD の3/40倍です。
今回用いた手順は、平面図形の演習をしっかりと重ねればそれほど意外な手順ではなくなると思います。
解き方のレパートリーを身に付けて、問題ごとに最適な解法を選べるように練習しましょう。
東京都 公立高校入試 数学 大問4 取り組む時期

数学の過去問は大問ごとに演習をすることをおすすめします。
まずは制限時間などは気にせず、しっかりと得点ができるかをチェックすることから始めましょう。
大問4に取り組むおすすめの時期は3年生の夏休みと冬休み。
3年生の夏休みにやること
合同の証明をしっかりと固めましょう。
都立入試の場合、証明問題の難度はそれほど高くありません。
中学2年生で習った合同の証明について、基本レベルをしっかりとさえましょう。
この時期はまだ過去問に取り組まなくても大丈夫です。
また、一つ一つの図をきちんと書くことを始めましょう。
図形問題の演習がうまく蓄積されるようになります。
合同の基礎固めが済んだ方は、
中学3年生範囲の先取りを進めましょう。
特に相似と円については、合同と同じレベルまで固めておけると良いです。
特に、平面図形のラスト問題が解けるようになりたい方は、
夏休み中に前単元の初見を終えておくことを強くおすすめします。
3年生の冬休みにやること
合同・相似の証明を徹底復習しましょう。
この段階でまだ証明に不安がある方は危険サインです。
少なくとも年内には基本問題が解けるようにしましょう。
基礎固めが終わったら、模試や入試の過去問で大問4の演習を始めましょう。
(1)、(2)①が安定して解けるかをチェックしてください。
図を書く習慣がついていない方は、ここが最後のチャンスと思って図を書き始めましょう。
問2② を得点したい人は、過去問の演習。
解法パターンを身に付けて、
例年よりも問題の難度が易しかった場合は必ず解ける
この状態を目指してください。
まとめ
東京都 公立高校入試 数学 大問4は平面図形です。
各小問で何が問われるのか把握して、できるだけ早い時期に得点が安定する状態まで持っていきましょう。
大問4の小問2題が解ければ入試の平均点はほぼクリアです。
それ以上のハイスコアを目指す際は問2② まで得点しましょう。
動画で解説
動画での解説もありますので、ぜひご覧ください。
東京都 都立高校入試 数学 全体の傾向と対策はこちら
「東京都 都立高校入試 数学 全体の傾向と対策」では大問1から5についての大まかな説明、61点を取るプランと78点を取るプランについて説明しています。
未読の方はぜひこちらも参考にしてください。



“東京都 公立高校入試 数学 大問4(平面図形)|図形が苦手でも点を取る考え方” に対して5件のコメントがあります。
コメントは受け付けていません。