2026年(令和8年度) 東京都立高校入試 数学 過去問 解説速報
※2026年度(令和8年度)東京都立高校入試 数学 過去問について、順次解説をupします!
はじめに
2026年度(令和8年度)東京都立高校入試問題 過去問 数学についての解説速報記事です。
高校受験の対策、学校の成績や模試の偏差値を上げるためにご活用ください。
※この記事は、林個別指導塾が運営する学習ブログです。
大問4
問1
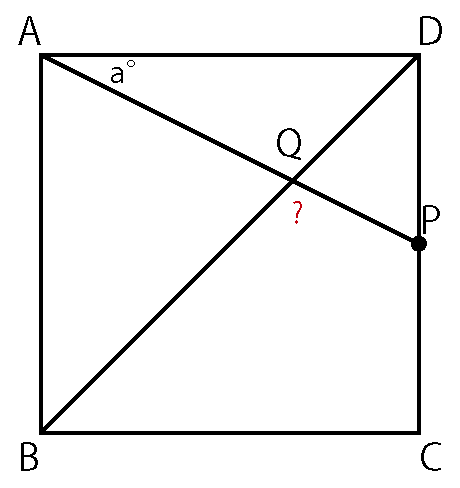
四角形ABCD は正方形
∠DAP = a°
∠BQP の大きさを求めよ。
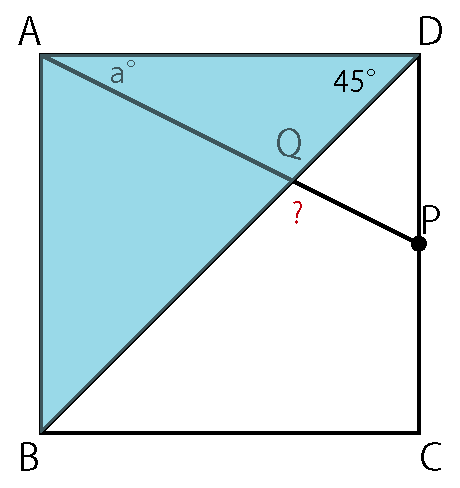
四角形ABCD は正方形なので、
△ABD は直角二等辺三角形
∠ADB = 45°
△AQD に着目すると、
∠AQD = 180° – (a + 45)°
= (135 -a)°
対頂角は等しいので
∠BQP = (135 – a)°
問3

四角形ABCD は正方形
AB = 12
PC = 3
BD // CS
線分PS の長さを求めよ。
相似な三角形をうまく見つけて、線分PS の長さを求めましょう。
線分PS が絡んだ三角形を使うことがコツです。

まず注目するのは、△DQP ∽ △CSP
BD // CS から見つけられる砂時計の形です。
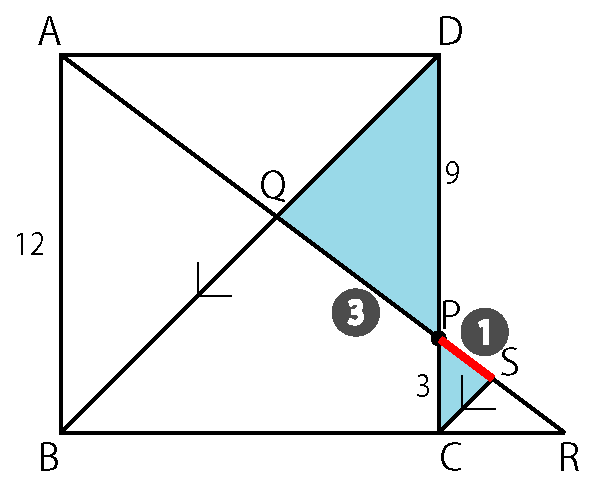
AP の長さは三平方の定理から求めることができるので、
次はAQ を比で表すことを目指します。
QP : SP = DP : CP より
QP を③, SP を①とおきます。
もちろんQP = 3a, PS = a のようにおいてもOKです!
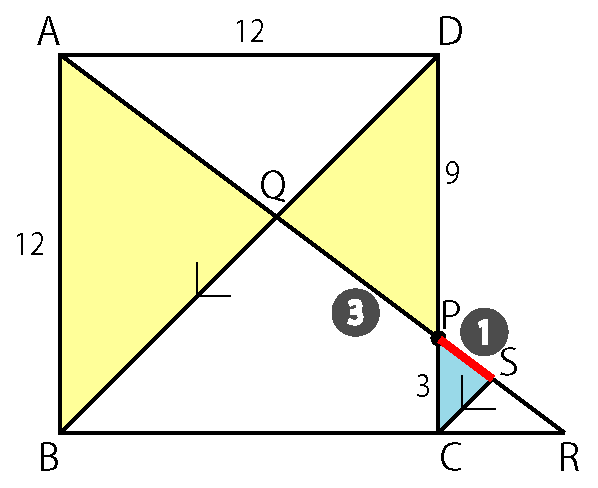
△ABQ ∽ △PDQ
これも砂時計の形です。
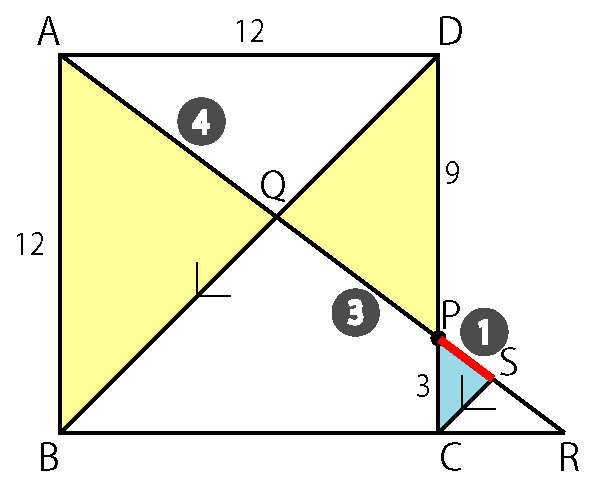
QP : QA = 3 : 4 より
QA は④と表すことができます。
AQ : QP : PC = 4 : 3 : 1
比を調整せずにそのまま使えるのはありがたいですね。
あとは仕上げ。
△APD は3 : 4 : 5 の直角三角形。
AP = 5 × 3 = 15
⑦が15 なので、① は 15/7
PS は15/7 となりクリアです!

