高校数学B「統計的な推測」 第5章|正規分布~標準正規分布表の使い方~ についてやさしく解説

正規分布の式は見た目が難しそうですが、使い方を覚えれば定期テストや共通テストでも得点源になります。
この記事では、正規分布の基本から標準正規分布表の活用法まで、例題や演習題を交えてわかりやすく解説します。
- 「正規分布って何?」
- 「標準正規分布表って何?」
- 「実際にどうやって問題を解くの?」
という疑問を持つ高校生・受験生の方は、ぜひここで基礎を固めて、
共通テスト数学の得点アップにつなげましょう!
正規分布とは?

一般的な正規分布
正規分布とは、平均値のまわりにデータが集まり、左右対称の「山なりの形」になる分布のことです。
平均から離れるほどデータが少なくなるのが特徴です。
平均値がμ、標準偏差がσ の正規分布は上のような関数で表されますが
この関数自体は覚えなくて大丈夫です!
覚えるべきは式の形ではなく、正規分布の特徴と使い方。
正規分布はx = μ(平均値)で最大値をとり、左右対称に山のように広がっている
ということをまずは覚えましょう。
特別な正規分布(標準正規分布)
正規分布のうち、平均が0・分散が1(標準偏差も1)のものを標準正規分布と呼びます。
先ほどよりもすっきりとした関数となりましたが、
やはりこの関数自体は覚えなくても大丈夫です。
重要なのは標準正規分布の特徴と使い方。
標準正規分布はx = 0(平均値)で最大値をとり、左右対称に山のように広がっています。
この標準正規分布の使い方を学ぶことが、この記事のテーマです。
定期テストや共通テストでは、この式を直接計算することはほとんどなく、
グラフの読み取りや標準正規分布表を使った確率の計算が中心です。
標準正規分布のグラフ
まずは正規分布のグラフの読み取りができるように、
グラフの形や縦軸・横軸の見方を確認しましょう!
標準正規分布のグラフの形
ベル型(釣鐘型)のグラフで、平均値を中心に左右対称に分布します。
平均から離れるほど確率が小さくなる特徴があります。
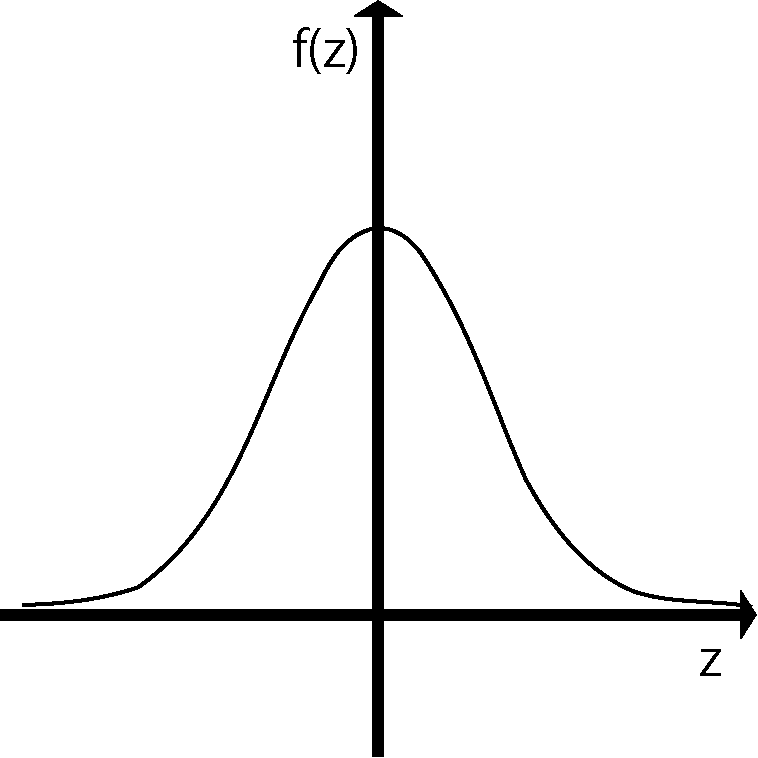
このグラフは平均値が0, 標準偏差が1 の標準正規分布です。
正規分布のグラフはどう読む?
正規分布のグラフは、平均値を中心に左右対称の山型をしています。
横軸は z値(z-score) といい、「平均からどれだけ離れているか(標準偏差の単位)」を表します。
縦軸は 確率密度(そのあたりに値が現れやすい度合い)を示します。
z値が大きくなるほど確率(その範囲の面積)は小さくなります。
ここではz値についてもう少し詳しく見ていきましょう。
例:
- z=0 … 平均と同じ値
- z=1 … 平均より標準偏差1つ分大きい値
- z=2 … 平均より標準偏差2つ分大きい値
68–95–99.7ルール
また、統計では特に z=1(約68%)、z=2(約95%) がよく使われます。
これは「平均から1標準偏差の範囲に約68%、2標準偏差の範囲に約95%のデータが含まれる」という経験則(68–95–99.7ルール)によるものです。
つまり、z=1やz=2は「どのくらいのデータが中心に集中しているか」を判断するための目安としてよく用いられます。

標準正規分布の場合
ある値が-1 以上 1 以下である確率が約68%
ある値が-2 以上 2 以下である確率が約95%
と考えることができます。
標準正規分布表って何?

ここまでで、標準正規分布の形と意味がわかりました。
ここからは様々な範囲のz値と確率の関係について解説をします。
たとえば:
- z値 が 0 以上 0.5 以下を取る確率は?
- 上位15%に入るには、z値 はいくつ以上?
このような問題を解く方法を説明します。
これらをクリアするために用いるものが標準正規分布表です。
標準正規分布表とは、
標準正規分布(平均値が0,標準偏差が1)が
z = 0 から0.01 刻みのz値に対応する確率を表にまとめたものです。
この表の数値を読み取ることで
- z値 が 0 以上 0.5 以下を取る確率は?
- 上位15%に入るには、z値 はいくつ以上?
先ほど例示したこれらの問題を、簡単に解くことができます。
標準正規分布表には2つのタイプがある
- タイプ①:0以上z以下の確率を示すもの 高校数学・共通テストで使用
- タイプ②:z以上右端(∞)までの確率を示すもの 統計学・実務統計などで使用
高校の教科書や共通テストでは、一般的にタイプ①(0以上z以下)を使います。この記事でもこのタイプを用います。
実際の標準正規分布表

この表の各マスの値が0以上z以下の確率を示すものです。
表を読む練習として、z値 が 0 以上 0.5 以下を取る確率を調べてみましょう。

この表の各マスの値が0以上z以下の確率を示すものなので、
z = 0.50 のときの値を探します。
6行1列目のマスの0.1915という値。
これがz値が 0 以上 0.5 以下を取る確率です。
つまり、求める確率は約19.2%(0.1915)ということ。

この表をうまく活用できるようになることが、この記事での目標です。
例題・演習題を通して、実際に出題される問題とその解法を確認しましょう。
例題:確率変数・標準正規分布表について理解を深めよう

※以下の問題では、確率変数 X は標準正規分布 に従うものとします。
※標準確率分布表は以下のものを使います。

確率を求める場合
確率変数Z が正規分布N( 0, 1 )に従うとき
P( -0.50 ≦ Z ≦ 0.50 ) について求めなさい。

初めのうちは、このようにグラフを書いて考えることをおすすめします。
今回のポイントは、0 ≦ z ≦0.5 ではなく-0.5 ≦ z ≦0.5 になっているところ。
標準正規分布表から読み取れるものは、が0以上z以下の確率でしたね。
0 ≦ z ≦0.5 の確率は表から読み取ることができるので、
残りの -0.5 ≦ z ≦0 の部分をどう処理するのか考えましょう。
ここで利用したいのが、
正規分布は平均値を軸として左右対称であるということ。
つまり、-0.5 ≦ z ≦0 の確率 と0 ≦ z ≦0.5 の確率は等しくなります。
z = 0.50 の数値を表から探すと、0.1915 とわかります。
なので
ある値が-0.50 以上0.50 以下である確率は約38.3% と分かりクリアです。
値を求める場合
確率変数Z が正規分布N( 0, 1 )に従うとき
値が低い方から20%の中に入るのは、いくつ以下の数値かもとめなさい。

グラフを書いて気づいてほしいことがふたつ。
まずは今回もz の値は負の数になりそうだということ。
もう一つは与えられた範囲が「0 からいくつかまで」の形式になっていないということ。
一つ目の問題は、正規分布のグラフの対称性を用いればクリア。
値が低い方から20% → 高い方から20%
と変換してあげればz値を正の数として扱えますね。

難しいのはもう一つの問題である、「0 からいくつかまで」の形式になっていないということ。
これは「0から□までの領域」を考えることで解決できます。
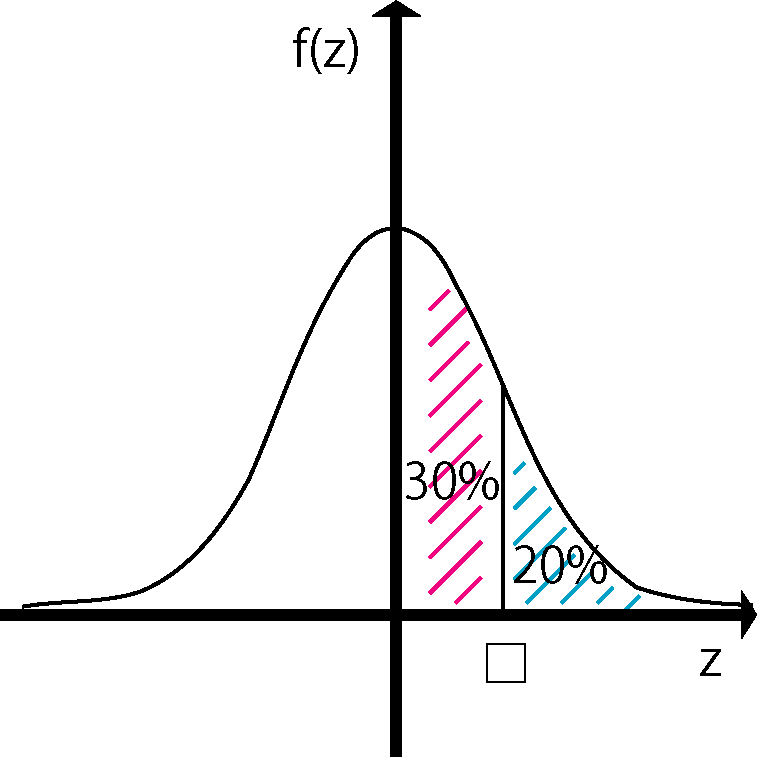
グラフの左右対称性より、z が0以上を取る確率は50%
Z が□ 以上の領域(青い部分)が20%であるということは、
z が0から□ までの領域(赤い部分)が30%ということ。
「z が0から□ までが30%」と変換してあげることで標準正規分布が使えます。
今回は確率が0.30に最も近いz値を、表から探しましょう。
z = 0.84 の時の値、0.2995 が0.30に最も近いです。
つまり、□に入る値は0.84
はじめにグラフを左右反転させたことも考慮すると、
値が低い方から20%の中に入るのは、-0.84以下であるとわかります。
標準正規分布表を活用するための工夫のパターンを身に付けましょう。
行るべき手順が見えやすくなるので、毎回グラフを書いて考えることをおすすめします。
例題の2パターンが自力で解けるようになったら、次は演習に進みましょう。
演習

※以下の問題では、確率変数 X は標準正規分布 に従うものとします。
※標準確率分布表は以下のものを使います。

確率を求める場合
確率変数Z が正規分布N( 0, 1 )に従うとき
P( -1.0 ≦ Z ≦ -0.50 ) について求めなさい。

標準正規分布表の値が活用できるように処理を行います。
z が0.50, 1.00 の値を表から探しましょう。
求める確率は、
つまり約15.0%
値を求める場合
確率変数Z が正規分布N( 0, 1 )に従うとき
値が低い方から40%の中に入るのは、いくつ以下の数値かもとめなさい。

値が低い方から40%に入るz値 を求めるためには
値が高い方から40%に入るz値 を考えればオーケーです。
□以上が40%であるならば、
0から□までは10%
f(z) が0.10 に最も近いz を表から探します。
f(0.25) = 0.0987 が、0.10 に最も近いです。
つまり、値が高い方から40%の中に入るz値は0.25以上ということ。
よって、値が低い方から40%の中に入るz値は-0.25以下と分かります。
標準正規分布表の活用はここから先の単元でも頻出なので、
スムーズに解けるまで繰り返し練習をしましょう。
まとめ
正規分布の導入として、
- 正規分布とはどのようなものか
- 正規分布のグラフの読み取り方
- 標準正規分布表の活用方法
これらについて解説を行いました。
正規分布表の活用をスムーズにこなすためには、問題演習の量をこなすことが重要です。
まずは表の読み取り方を覚えて、
さらにそれがスムーズになるように繰り返し問題を解きましょう!
次回は「第6章|正規分布~標準化の使い方~」です。
「平均が0, 分散が1 ではない正規分布」を標準化して、標準正規分布で扱う方法を学びます。
正規分布と標準正規分布表の確認テスト|この章の理解はバッチリ?
以下のポイントが自力で説明・再現できれば、この章はほぼマスターです!
- 正規分布とはどのような分布か
- z値とは何か
- 標準正規分布表とは何か
- 標準正規分布表の活用法
「ちょっと怪しいかも…」と思った箇所があれば、上に戻って再チェックしてみましょう!
◀ 第4章|二項分布・ベルヌーイ分布
▶ 第6章|正規分布~標準化の使い方~
▶︎高校数学B「統計的な推測」シリーズ目録・過去問解説のまとめはこちら!
共通テスト・大学入試に向けて勉強を始めたい方は、林個別指導中にお問い合わせください。
無料のオンライン体験授業も用意しております!



“高校数学B「統計的な推測」 第5章|正規分布~標準正規分布表の使い方~ についてやさしく解説” に対して7件のコメントがあります。
コメントは受け付けていません。