高校数学B「統計的な推測」第4章｜二項分布・ベルヌーイ分布の使い方 をやさしく解説

「二項定理は聞いたことがあるけど二項定理ってなんだっけ？」

これら二つは名前が似ているためか、意味がごっちゃになっている生徒をよく見かけます。

このページでは、「二項分布・ベルヌーイ分布の使い方」について、
例題を通してわかりやすく解説します。

という疑問を持つ高校生・受験生の方は、ぜひここで基礎を固めて、
共通テスト数学の得点アップにつなげましょう！

二項分布・ベルヌーイ分布とは？

今回のメインテーマである二項分布とベルヌーイ分布。
まずはそれぞれの定義について確認をしましょう。

二項分布とは？

二項分布は、同じ確率で繰り返される試行をn回行ったとき、「成功した回数」が従う確率分布です。

例えば…

• コインを10回投げて、表が出た回数
  ➥コインの表が出る確率は1/2、これを10回繰り返している
• 赤玉が2個、白玉が3個入っている箱から球をひとつ取り出して元に戻す。これを５回行ったときに白玉を引いた回数
  ➥白玉を引く確率は3/5、これを5回繰り返している

これらの問題を解く際に使用するものが二項分布の考え方です！

ベルヌーイ分布とは？

ベルヌーイ分布は、成功か失敗かの1回の試行だけに注目した確率分布です。

• コインを1回投げる
• 箱から球を1回だけ引く

１回の試行だけというところがポイントです。

このベルヌーイ分布をn回繰り返すことで、先ほどの二項分布につながっていきます。

二項分布とベルヌーイ分布の関係は？

二項分布 … 同じ確率で繰り返される試行をn回行ったとき、「成功した回数」が従う確率分布

ベルヌーイ分布 … 成功か失敗かの1回の試行だけに注目した確率分布

どちらも同じ試行について扱っており、違うのは回数だけ！

つまり、
ベルヌーイ分布をn回繰り返す → 二項分布になる
ということです！

二項分布の公式

これまで、期待値・分散・標準偏差を求めるためにはいくつかの手順が必要でしたね。

しかし二項分布の期待値や分散・標準偏差は、
公式を用いて簡単に求めることができます。

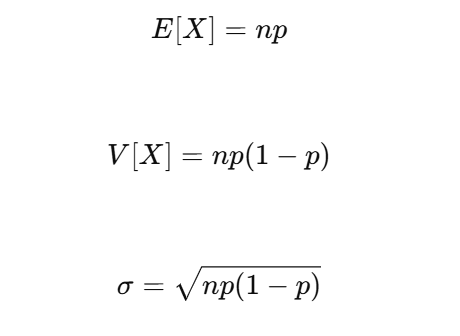
• n は試行回数（コインを何回投げたか）
• p は成功する確率（コインの表が出る確率）

さらにq = 1 – p (q は失敗する確率)で公式をまとめると…

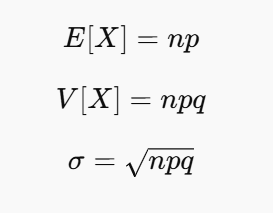
このように公式を書き換えることができます。

• 期待値は 試行回数 × 成功する確率
• 分散は 試行回数 × 成功する確率 × 失敗する確率

このように言葉でも覚えやすくなりますね。

これらの公式の成り立ちが気になる方は、
「二項分布の期待値・分散・標準偏差の公式の証明方法」コラムをチェックしてください！

[高校数学B] 二項分布の期待値・分散・標準偏差の公式の証明方法をやさしく解説

二項分布を覚えるメリットは？

これまで期待値・分散・標準偏差を求めるときには、
確率分布を表にまとめて計算する方法を取っていました。

「そのやり方を使えばわざわざ二項分布の公式を覚えなくてもよくない？」
という疑問をここで解消しておきましょう。

二項分布の公式を覚えるメリットは主に２つあります。

より詳しく知りたい方は以下のコラムをチェックしてください。

二項分布を覚えるメリットの詳しい解説と、
実際の問題演習を「確率分布をまとめる方法」と「公式を活用する方法」の２パターンで比較しています。

高校数学B「統計的な推測」二項分布を覚えるメリットは？｜やさしく解説

二項分布以外の分布は？

二項分布以外にもいろいろな分布とその公式が存在します。

いくつか確率分布とその具体例をあげます。

高校数学では二項分布と正規分布についてじっくり勉強をしますが、
それ以外にもいろいろな分布が存在します。

この中で特に「ポアソン分布」について記事をまとめています。
興味のある方はぜひチェックしてください！

[高校数学B] ポアソン分布って何？｜高校生にもわかりやすく解説！

以上を踏まえて、ここからは実際に例題に触れて、解答の手順をチェックしましょう。

例題：二項分布の公式を活用しよう

実際に公式を使って問題を解く流れをチェックしましょう。

例題：コインを5回投げる

二項分布に従うかチェック

今回の問題は、
成功する事象（表が出る）が毎回同じ確率で起こります（$\frac{1}{2} の確率で表が出る$）。

よってこれは二項分布です！

n, p, q を求める

n … 試行回数

p … 成功する確率

q … 失敗する確率

まずは文章の情報をもとに、これらを求めましょう。

コインを５回投げるため $n=5$

表が出る確率 $p=\frac{1}{2}$

裏が出る確率 $q=\frac{1}{2}$

公式で期待値・分散・標準偏差を求める

これらを公式に代入すると

$E[X]=np$

$=5 \times \frac{1}{2}$

$=\frac{5}{2}$

$V[X]=npq$

$=5\times \frac{1}{2} \times \frac{1}{2}$

$=\frac{5}{4}$

$σ=\sqrt{npq}$

$=\frac{\sqrt{5}}{2}$

例題：サイコロを10回投げる

二項分布に従うかチェック

今回の問題は、
成功する事象（３の目が出る）が毎回同じ確率で起こります（$\frac{1}{6} の確率で表が出る$）。

よってこれは二項分布です！

n, p, q を求める

n … 試行回数

p … 成功する確率

q … 失敗する確率

まずは文章の情報をもとに、これらを求めましょう。

サイコロを10回投げるため $n=10$

３の目が出る確率 $p=\frac{1}{6}$

３以外の目が出る確率 $q=\frac{5}{6}$

公式で期待値・分散・標準偏差を求める

これらを公式に代入すると

$E[X]=np$

$=10 \times \frac{1}{6}$

$=\frac{5}{3}$

$V[X]=npq$

$=10\times \frac{1}{6} \times \frac{5}{6}$

$=\frac{25}{18}$

$σ=\sqrt{npq}$

$=\frac{5\sqrt{2}}{6}$

解法の流れ

まずは問われているものが二項分布に従うかどうかを確認しましょう。

二項分布に従っていれば公式を使う準備。
n, p, q を求めます。

それらを用いて公式から期待値・分散・標準偏差を求めてクリアです！

演習

この問題は赤い球を取り出すか白い球を取り出すかのどちらかが、毎回同じ確率で起こる。つまり二項分布に従います。

この問題も、二項定理の公式を使って解いてみましょう。

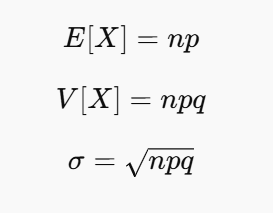
試行回数 $n=20$

赤い球を取り出す確率 $p=\frac{3}{10}$

白い球を取り出す確率 $q=\frac{7}{10}$

これらを公式に代入して求めます。

$E[X]=np=6$

$V[X]=npq=\frac{21}{5}$

$σ=\sqrt{npq}=\frac{\sqrt{105}}{5}$

期待値は6回、標準偏差は√105 / 5 と分かります。

まとめ

例題、演習題を交えて二項分布について解説を行いました。

まずは二項分布とは何か、自分で説明できるように！
二項分布は、同じ確率で繰り返される試行をn回行ったとき、「成功した回数」が従う確率分布でしたね。

次に二項分布の公式をしっかりと覚える。
そしてそれを活用できるように練習する。

演習問題が自力で解けるように練習をしましょう。

次回は「第５章｜正規分布～標準正規分布表の使い方～」です。

二項分布・ベルヌーイ分布｜この章の理解はバッチリ？

以下のポイントが自力で説明・再現できれば、この章はほぼマスターです！

• ベルヌーイ分布とは何か説明できるか
• 二項分布とは何か説明できるか
• 二項分布の期待値、分散、標準偏差を求める公式を書き出せるか
• 公式を使うメリットを説明できるか
• 実際に公式を用いて演習題を自力で解けるか

「ちょっと怪しいかも…」と思った箇所があれば、上に戻って再チェックしてみましょう！

---

◀ 第３章｜確率変数の変換 Y = aX + b の期待値・分散
▶ 第５章｜正規分布～標準正規分布表の使い方～

▶︎高校数学B「統計的な推測」シリーズ目録・過去問解説のまとめはこちら！

---

共通テスト・大学入試に向けて勉強を始めたい方は、林個別指導中にお問い合わせください。

無料のオンライン体験授業も用意しております！

▶︎ [公式LINEに登録する]
▶︎ [お問い合わせフォームへ]