[高校数学B] ポアソン分布って何？｜高校生にもわかりやすく解説！

「ポアソン分布（Poisson distribution）」って聞いたことはありますか？

名前だけは聞いたことがあるけど、実際にはよく知らない──そんな人も多いかもしれません。

実際、高校数学の授業では「ポアソン分布」はあまり扱われません。高校数学B「統計的な推測」に登場するのは主に「二項分布」や「正規分布」などです。

ですが、「高校で習うもの以外に、どんな分布があるの？」「名前がかっこいいから気になる！」という好奇心から入ってもまったく問題ありません。

このコラムでは、“まれにしか起こらない現象の回数”を扱うときに登場する「ポアソン分布」について、簡単な例題も交えてやさしく解説します。

ポアソン分布とは簡単に

ポアソン分布とは、ある一定の時間や空間内に「まれに起こる出来事」の発生回数を確率的に扱う分布のことです。

例えば、「1時間に何件の地震が起こるか？」や「10分間に何人のお客さんが来るか？」といった問題で使われます。

ちなみに「ポアソン」という名前は、19世紀フランスの数学者シメオン・ドニ・ポアソンにちなんで名付けられました。

ポアソン分布はどんな場面で使う？

地震の回数

あなたが暮らしている地域で、「地震って1日にどれくらい起こってるんだろう？」とふと思ったことはありませんか？

もちろん、毎日地震があるわけではありません。でも、ときどき「1日で3回も揺れた」という日があったりします。

このように、たまにしか起きないけど、いつ起こるかは予測しづらい現象を扱うとき、ポアソン分布がぴったりです。

コンビニに来るお客さんの人数

ある深夜のコンビニ。普段は静かで人も少ないのに、突然5人連続で来店する──そんなこともあります。

「1時間で何人来るか」は日によってばらつきがありますが、平均的には1時間に2〜3人と決まっているとしましょう。

このような、「平均的な来店人数はわかるけど、ぴったり何人来るかはランダム」という状況も、ポアソン分布で表せます。

ポアソン分布を数式で見る

ここからはポアソン分布が実際どのような式なのかを見ていきましょう。

ポアソン分布は次のような特徴を持ちます：

• 試行回数：無限大（または非常に多い）
• 成功確率：ごく小さい
• 平均回数：一定（ と表す）

このとき、 回起こる確率は次のように表されます：

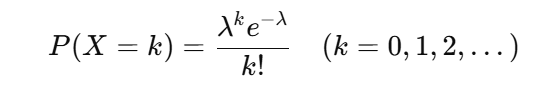
ここで：

• λ ：単位時間あたりの平均発生回数
• e ：ネイピア数（自然対数の底、約2.718）

どちらもあまり見慣れない文字かもしれませんが、その文字が何を表しているのかをよく覚えておきましょう！

例題：ポアソン分布の使い方

ポアソン分布の考え方、そして先ほどの数式を使ってどのように問題を解くのか。

例題を通して解説します。

例題：あるバス停に10分間で平均2人が来るとき、10分間でちょうど3人来る確率は？

λ とk に何を代入すればよいのかを考えましょう。

• 10分で平均2人来る → λ = 2
• 10分で3人来る確率 → k = 3

これを公式に当てはめて代入すると：

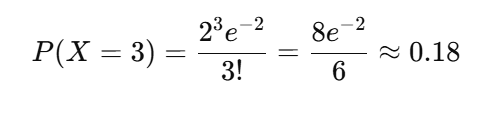
あるバス停に10分間で平均2人が来るとき、10分間でちょうど3人来る確率は約18%と分かります。

演習：実際にポアソン分布を使ってみよう！

先ほどの例題と同様に、今度は自力で演習題を解いてみましょう。

• ポアソン分布の公式を書きだす
• λ と k に何を代入するか考える

この手順で解けば間違え無しです！

演習①：1日に平均1.5回の地震が起こる地域で、ある日にちょうど2回の地震が発生する確率は？

この場合：

• 1日あたりの平均発生回数 → λ = 1.5
• 起こる回数 → k = 2

これをポアソン分布の公式に代入すると：

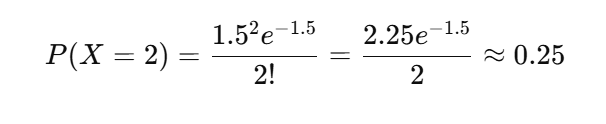
約25%！

演習②：ある深夜のコンビニで、1時間に平均3人のお客さんが来るとき、2時間でちょうど5人来店する確率は？

2時間では平均来店人数が λ = 3 × 2 = 6 に変化します

求めたいのは、2時間でちょうど5人来る確率 → k = 5

ポアソン分布では、時間や空間の長さが変われば、その分 λ もスケーリングすることで対応できます。

これを公式に当てはめて計算すると：

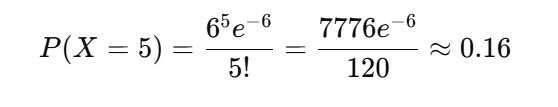
約16%!

まとめ

ポアソン分布について高校生にもわかりやすく解説しました。

ポアソン分布は：

• 二項分布の仲間
• 回数を扱う分布
• 平均 λ さえわかれば計算できる

高校数学では深く扱いませんが、将来、統計・AI・医療などを学ぶなら必須知識です。

これを機にポアソン分布への理解を深めましょう！

---

▶︎ 高校数学B「統計的な推測」シリーズ全体の目録はこちら！

共通テスト・入試に向けて学習プランを立てて取り組みたい方は、学習相談・入塾相談などお気軽にお問い合わせください。

▶︎ [公式LINEに登録する]
▶︎ [お問い合わせフォームへ]