[高校数学Ⅰ] 二次関数 計算間違えをしない平方完成のやり方をやさしく解説！

次の二次関数を平方完成せよ

高校数学では定番の問題ですが、意外と手順が多くて大変ですよね。

なんとなくやり方はわかるけど、x² の係数が1以外の時はどうすればよかったっけ…

平方完成は多くの高校生がつまづいてしまうポイントです。

この記事では「二次関数の平方完成」について、数学が苦手な生徒に向けてやさしく解説します。

これらの疑問ついて解決して、定期テストや共通テストで高得点を目指しましょう！

※この記事は、林個別指導塾が運営する学習ブログです。

平方完成とは？

平方完成とは、2次式（ax² + bx + c）の形を、(x + p)² + q のように「平方の形」に変形することを指します。

たとえば、

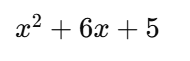
という式は、以下のように変形できます。

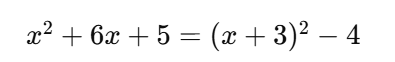
この変形のテクニックが「平方完成」です。

なんで平方完成が必要？

そもそもなんで平方完成しないといけないの？

それなりに大変な手法を会得するのであれば、先にそのメリットを知りたいですよね。

平方完成を使うと、次のようなメリットがあります。

1. グラフの頂点がわかる

2次関数を平方完成すると、グラフの頂点がどこにあるのかがすぐにわかります。

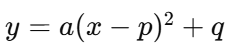
この場合、頂点は(p, q) と分かります。

グラフを描く際に頂点の把握は必須ですね。

2. 最大・最小値がわかる

平方完成の結果から、関数の最大値や最小値を簡単に読み取ることができます。

二次関数の最大値・最小値の求め方は以下の記事で詳しく解説しています。

[高校数学Ⅰ] 二次関数 最大値・最小値の求め方をやさしく解説！

3. 解の公式の導出につながる

2次方程式の解の公式（いわゆる「因数分解できないときに使うやつ」）も、もとをたどると平方完成の考え方から導かれています。

解の公式を導出する際にも平方完成のスキルが必要です。

---

平方完成は、高校数学だけでなく、大学入試や物理・経済学などの分野でも活躍する重要な考え方です。

これから先いろいろなところで登場する平方完成を、ぜひ今のうちにクリアしておきましょう！

計算間違えをしない、平方完成のやり方

毎回同じ手順で計算する

平方完成で計算ミスをしてしまう一番の原因は、「毎回の手順が定まっていない」ことです。

数値・パターンによってやり方を変えてしまうとフォームが定まらず、スムーズに解けないうえに計算ミスの確率が増してしまいます。

以下に説明する手順を覚えて、実践できるようにしてください！

1. 式を書く

まずは平方完成する式を書くことから。

係数の見間違えを防ぐためにも、平方完成する式を1行目にきちんと書きましょう。

2. x²の係数でくくる

x²の係数でくくります。

この時にくくるのはx², x の項まで。
定数項はくくらなくて大丈夫です。

x² の係数が分数の場合は特に計算ミスが起きやすいので、一度展開して元の式に戻るか必ず確認してください。

3. かっこ内を平方完成

中かっこを使って平方完成。

x² + 2x を平方完成するためには +1 が足りない。

なので、(x² + 2x + 1) – 1 として(x + 1)² を作りましょう！

4. 中かっこを外す

係数2 を(x + 1)², -1 に分配して中かっこを外します。

定数項 -3 の書き忘れに注意しましょう！

5. 定数項を整理

-2 -3 = -5
定数項を整理して完成です。

最後に、平方完成を展開したらはじめの式に戻るかを必ずチェックしましょう。

もしも元も式に戻らない場合は途中式を一つずつチェック。
これで計算ミスを防ぐことができます！

はじめのうちは途中式を飛ばさずにきちんと手順を守ることを意識してください。

＋α｜手順に慣れてきたら…

基本的な計算は、できる限り少ない手数、少ない時間でこなしたいですよね。

平方完成の手順に慣れてきたら少しずつ途中式を減らしましょう。

平方完成ができたら展開して元の式に戻るか必ずチェック！

途中式を減らす際に気を付けること

基本的な手順は完璧に理解してる。
そのうえで式を省略してもスムーズに解ける。
そう確信したときに途中式を減らし始めましょう。

途中式を書くことが面倒だからといって、十分に身についていない状態で式を省略することはNGです。

途中式を外したせいでかえって時間がかかってしまう、計算が不正確になってしまう、となってしまっては本末転倒ですよね。

より少ない時間でこなすために途中式を省略する。

これは平方完成に限らず、どの問題の手順習得の際にも気を付けることです！

練習問題

以下の3問について、上で説明した手順を意識して平方完成してみましょう！

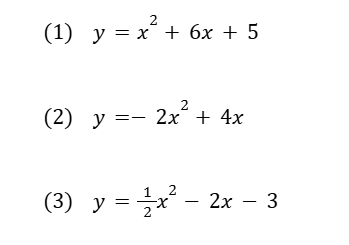
(1) の解き方

(1) はx² の係数が1のパターン。x² の係数でくくる必要がないだけで後はすべて手順通り。

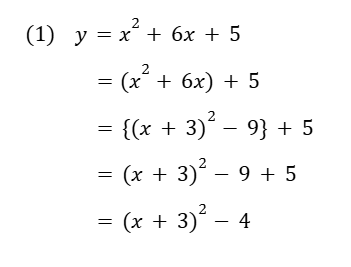
(2) の解き方

(2) ははじめに与えられた式に定数項がないパターン。このような微妙な例外に惑わされることなく、必要のない手順は飛ばす、を意識してください！

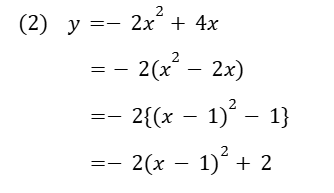
(3) の解き方

(3) はスタンダードなパターン。これは難しい… ではなく、これがスタンダードと思うようにしましょう！

---

どの問題も手順を守って解けましたか？

答えが間違ってしまっても今は大丈夫。
まずは手順をしっかり守って演習を蓄積しましょう！

まとめ

平方完成とは何か、平方完成のメリット、そして計算間違えをしない平方完成の手順について解説をしました。

学校のワークや課題で繰り返し平方完成の練習をして、定期テストや大学入試で得点できるように準備をしましょう！

平方完成の確認テスト｜この記事の理解はバッチリ？

以下のポイントが自力で説明・再現できれば、この記事はほぼマスターです！

• 平方完成って何？
• 平方完成ってどうしてするの？
• 計算ミスをしない平方完成の手順は？

「ちょっと怪しいかも…」と思った箇所があれば、上に戻って再チェックしてみましょう！

次に読むべき記事｜数学Ⅰを苦手から得意に！

平方完成が完璧になったら、次は二次関数の最大値・最小値について学習をしましょう。

以下の記事で二次関数の最大値・最小値について詳しく解説をしています。

一つずつクリアして、数学を苦手から得意に変えましょう！

[高校数学Ⅰ] 二次関数 最大値・最小値の求め方をやさしく解説！

高校数学に不安がある方へ

高校数学について不安がある方、共通テスト・入試に向けて学習プランを立てて取り組みたい方は、学習相談・入塾相談などお気軽にお問い合わせください。

▶︎ [公式LINEに登録する]
▶︎ [お問い合わせフォームへ]