高校数学B「統計的な推測」 中心極限定理って何？｜やさしく解説

この記事では中心極限定理とは何なのか、高校生にもわかりやすく解説をします。

という疑問を持つ高校生・受験生の方は、
ぜひここで基礎を固めて、統計的な推測への理解を深めましょう！

中心極限定理とは？

確率や統計の分野でとても重要な考え方が、中心極限定理（Central Limit Theorem：CLT） です。
これは一言で言うと、

「ランダムなものをたくさん足すと、結果の分布は正規分布に近づく」

という法則です。

【直感的な説明】

サイコロを1個振ると、1〜6のどれもが同じ確率で出ます。

振るサイコロを2個に増やすとどうなるでしょう？

出た目の「和」を考えると、7が一番出やすく、2や12は出にくくなります。

さらにサイコロを3個、4個と増やしていくと、ますます「真ん中の値が出やすく、両端は出にくい」形になっていきます。

このように、ランダムなものをいくつも足すと、中央に山を持つなだらかな分布（正規分布の形）に近づいていくのです。

【数学的な定理としての形】

平均が μ、分散が σ² の確率変数 X1 ,X2, …, Xn​ が独立に存在するとします。

それらの平均を

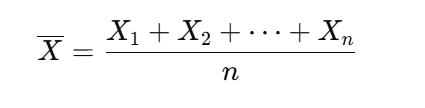
としたとき、

次の量

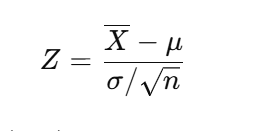
は、n が大きくなると標準正規分布N(0,1) に近づきます。

つまり、「平均からのズレを標準化したもの」が、試行を増やすほど正規分布の形に収束するのです。

グラフの形が正規分布っぽくなるだけ？

サイコロをいくつも投げると真ん中の数が最も多く出て、端の数はあまり出ない。
だからなんとなく正規分布っぽいグラフの形になる。

ここまではイメージが付きやすいと思います。

しかし実は、これは「なんとなく正規分布っぽい形になる」だけではありません。

「なんとなく似ている」ではなく、数学的に正規分布になることが証明されています。

これは偶然ではなく、「確率変数の和（または平均）」の性質によるものです。

• たくさんの独立な確率変数を足すと、平均から大きく離れるケースはどんどん減る
• その結果、中央の値が多く、両端が少ない形になる
• この「集まり方」が、実際に正規分布関数そのものに一致することが数学的に示されている

証明には「特性関数」や「モーメント母関数」という大学数学の道具を使いますが、
高校生の段階では「たくさん足すと正規分布になる」という結果を理解できれば十分です。

中心極限定理と二項分布

中心極限定理の代表的な応用が、二項分布の正規分布による近似です。

二項分布 B(n,p)は、成功・失敗のような「2択の結果」を繰り返したときの成功回数を表す分布でしたね。

試行回数 n が大きいとき、二項分布は次の正規分布に近づきます。

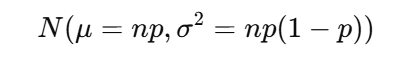
これはまさに中心極限定理の結果です。

個々の試行（成功 or 失敗）は独立で、たくさん足し合わせた結果（成功回数）が正規分布に近づくのです。

大数の法則とのちがい

「中心極限定理」について学習するタイミングで「大数の法則」というものも目にした方が多いのではないでしょうか。

これら二つの法則は意味を混同しやすいので、ここで簡単に整理しておきましょう。

「たくさん集めると平均が母平均に近づく」という話が大数の法則です。

一方で、「その平均の分布の形が正規分布に近づく」というのが中心極限定理です。

つまり、

• 大数の法則：平均が母平均に近づく
• 中心極限定理：平均の分布が正規分布に近づく

という関係になっています。

これら二つの違いを覚えておくと学習がよりスムーズになるので、ぜひ覚えておいてください！

まとめ

中心極限定理について直感的な説明を絡めて解説を行いました。

ランダムの積み重ねは正規分布になる。

中心極限定理について簡単に説明できるようにしておきましょう。

---

▶︎ 高校数学B「統計的な推測」シリーズ全体の目録はこちら！

共通テスト・大学入試に向けて勉強を始めたい方は、林個別指導中にお問い合わせください。

無料のオンライン体験授業も用意しております！

▶︎ [公式LINEに登録する]
▶︎ [お問い合わせフォームへ]