高校数学B「統計的な推測」 第7章|正規分布~二項分布の近似~ やさしく解説

二項分布は確率の計算を行う上でとても強力な武器です。
ただし試行回数が多い場合、二項分布の公式では立式はできるけれど計算ができないというケースが発生します。
この記事では、試行回数が多い二項分布をどのように処理すればよいのかについて、具体例を用いてわかりやすく解説します。
- 「二項分布って何?」
- 「二項分布ってどうやって使う?」
- 「試行回数が多い二項分布はどうする?」
- 「二項分布と正規分布の関係は?」
という疑問を持つ高校生・受験生の方は、ぜひここで基礎を固めて、
共通テスト数学のスコアアップにつなげましょう!
二項分布とは?(復習)
二項分布の公式
二項分布とは、成功・失敗の2つの結果しかない試行をn回行ったとき、成功が何回起こるかを表す確率分布です。
コイン投げや合格・不合格のような「2択の確率」を扱うときによく登場します。
二項分布の確率は次の式で表されます。
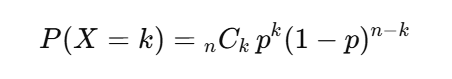
ここで
- n:試行回数
- p:1回の成功確率
- k:成功の回数
です。
この分布は、p=0.5 のとき左右対称になり、p が0や1に近いときは偏った形になります。
二項分布についてもっと詳しく復習したい方は、以下の記事をチェックしてください!
二項分布の期待値・分散・標準偏差
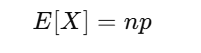
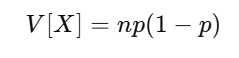
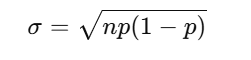
二項分布は期待値・分散・標準偏差を公式で求めることができましたね。
これら公式の導出を復習したい方は以下の記事をチェックしてください!
例題:二項分布を活用
二項分布を活用することで様々な確率を求めるための立式ができます。
ただし、その立式が実際に計算できるかどうかはまた別の話…
ここでは立式はできるが計算が大変(実質できない)ケースがどういうものか紹介します。
計算可能かどうかの決め手となるものは試行回数。
試行回数が少ない場合と多い場合のそれぞれについて、実際に例題を解いてみましょう。
試行回数が少ない場合
表と裏が出る確率がともに1/2であるコインを5回投げる。
このとき表が3回以上出る確率を求めなさい。
解いてみる
確率変数X をコインを5回投げた時に表が出る回数とします。
表が3回以上出る確率→3回出る確率 + 4回出る確率 + 5回出る確率 という考えで解きます。
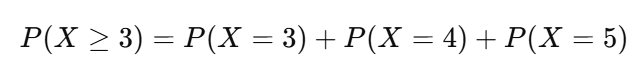
それぞれの確率は二項分布の公式で式が立てられますね。
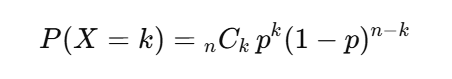
それぞれの確率を実際に計算すると…
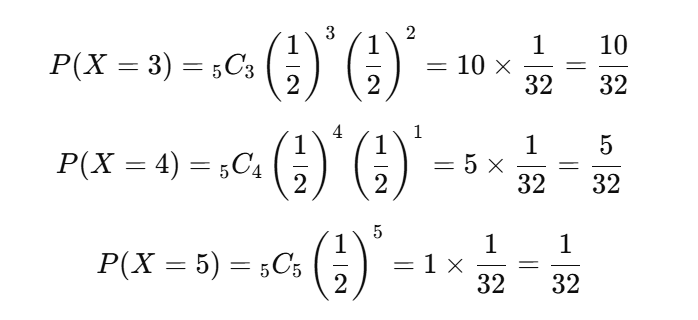
よって
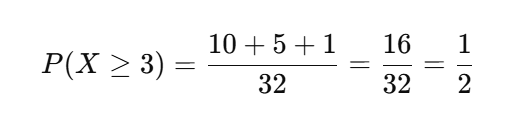
このようにして、試行回数が少ないときであれば二項分布を使って簡単に解くことができます。
ここまではすでに学習した内容ですね。
次は試行回数が多い場合について見ましょう。
試行回数が多い場合
表と裏が出る確率がともに1/2であるコインを100回投げる。
このとき表が56回以上出る確率を求めなさい。
解いてみる
確率変数X をコインを100回投げて表が出る回数とします。
表が56回以上出る確率→56回出る確率 + 57回出る確率 + … + 100回出る確率 という考えで解きます。
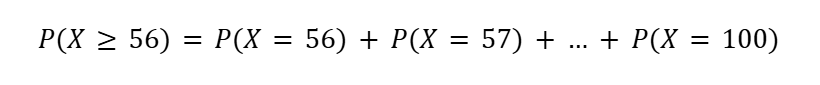
一つ一つの確率は二項分布の公式で立式できます。
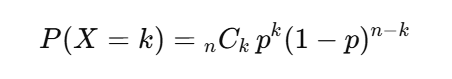
まずは表が56回出る確率について計算すると…
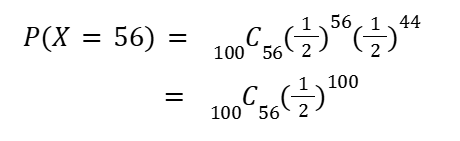
ここまで立式することはできますが、この後の計算ができないですね…
仮にものすごく頑張ってこの計算をしたとしても、まだ表が57回、58回…と計算すべきものが残っています。
このように 試行回数(n)が大きいとき、二項分布をそのまま扱うのは現実的ではありません。
ではどうすれば計算ができるのか…
ここで登場するのが 正規分布による近似 です。
二項分布の正規分布による近似
二項分布は、試行回数 n が大きくなると、平均 μ = np、分散 σ² = np(1−p) をもつ正規分布に近づくという性質があります。
この性質を活用して先ほど計算に詰まった問題を解いてみましょう。
表と裏が出る確率がともに1/2であるコインを100回投げる。
このとき表が56回以上出る確率を求めなさい。
二項分布の平均と標準偏差を公式から計算します。
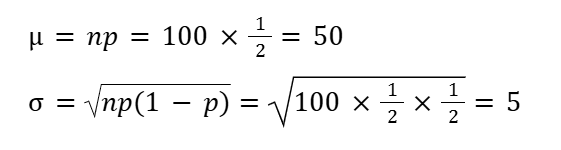
二項分布を正規分布へ近似すると…
この二項分布は 正規分布(50, 5²)に近似することができます。
確率変数X をコインを100回投げて表が出る回数とします。
表が60回以上出る確率を求めるために標準化を用いましょう。
新たに確率変数Z を定義して、それが標準正規分布 N(0, 1²) に従うように調整することが標準化でしたね。
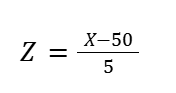
この変換によって標準正規分布表を用いることができます。
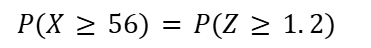
こうすれば、表が56回出る確率・57回出る確率と一つずつ計算をせずとも確立を求めることができます。
標準正規分布表を読み取って、求める確率を算出しましょう。

標準正規分布表を読み取ると
f(1.2) = 0.3849
よって、

コインを100回投げて表が56回以上出る確率は約11.5% です。
近似を使うときの条件
正規分布で近似できるのは、次の条件が満たされているときです。
- n が十分大きい(目安:30以上)
- np≥5 かつ n(1−p)≥5
これらの条件を満たしていれば二項分布の形は正規分布にかなり近くなり、正規分布への近似を行うことができます。
ただし共通テストにおいては、標本(nの値)が十分に大きいなどの記述が書かれていれば正規分布への近似を用いて大丈夫です。
なぜ正規分布への近似ができるの?
なぜ二項分布を正規分布へ近似できるのかについて、簡単に解説をします。
試行回数が多くなると、分布の形がなめらかになるから
たとえば、コインを1回投げたら結果は「表か裏」。
2回なら「表が0回〜2回」。
5回なら「0〜5回」。
…と、成功回数(表の回数)は少しずつ広がっていきます。
では、100回投げたら?
このときの「表の出る回数」を棒グラフにしてみると、
真ん中の50回あたりが最も高く、両端(0回や100回)はほとんど起こらない形になります。
このグラフの形が、だんだん正規分布の「山型」に近づいていくのです。
「たくさんの小さな偶然が重なる」から
1回ごとのコイン投げは完全にランダムですが、
50回、100回と増えていくうちに、「たくさんの偶然の積み重ね」が平均的な形を作ります。
これは「中心極限定理」という考え方で、
たくさんの独立したランダムな出来事を足し合わせると、全体は正規分布に近づくという性質があります。
つまり、「成功回数の合計(= 二項分布)」も、このルールに従って正規分布の形に近づくのです。
中心極限定理については以下のコラムに高校生にもわかりやすくまとめています。気になる方はぜひチェックしてください!
演習:二項分布を正規分布で近似してみよう
表と裏が出る確率がともに1/2であるコインを100回投げる。
このとき表が45回以上55回以下となる確率を求めなさい。
解法
これも二項分布の公式では「立式はできるけど計算はできない」パターンですね。
このようなときは正規分布への近似を用いましょう。
準備として、二項分布の平均と標準偏差を公式から計算します。
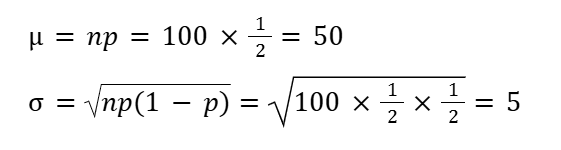
二項分布を正規分布へ近似すると…
この二項分布は 正規分布(50, 5²)に近似することができます。
確率変数X を表が出る回数とします。
表が45回以上55回以下で出る確率を求めるために標準化を用いましょう。
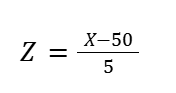
この変換によって標準正規分布表を用いることができますね。


標準正規分布表を読み取ると
f(1.0) = 0.3413
よって、
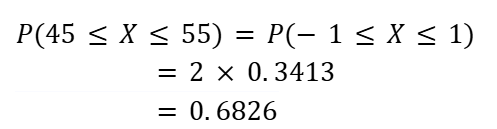
コインを100回投げて表が45回以上55回以下となる確率は約68.3%です。
まとめ:試行回数が多い二項分布は、正規分布へ近似!
試行回数が多い二項分布は、正規分布へ近似して確率の計算を行うことができます。
まずはそのことをしっかりと覚えて、例題・演習題を通して実際の解法をつかみましょう。
二項分布と正規分布はまったく別の概念ではなく、規模が大きくなると正規分布に収束するということをよく覚えておいてください。
この理解が、「統計的な推測」で学ぶ母集団と標本の関係にもつながっていきます。
二項分布と正規分布の確認テスト|この章の理解はバッチリ?
以下のポイントが自力で説明・再現できれば、この章はほぼマスターです!
- 二項分布の公式が書けるか
- 試行回数が多い二項分布はどうするか
- なぜ二項分布は正規分布に近似できるか
- 中心極限定理を簡単に説明できるか
「ちょっと怪しいかも…」と思った箇所があれば、上に戻って再チェックしてみましょう!
◀ 第6章|正規分布~標準化の使い方~
▶ 第8章|母集団と標本~標本平均の期待値と標準偏差~
▶︎高校数学B「統計的な推測」シリーズ目録・過去問解説のまとめはこちら!
共通テスト・大学入試に向けて勉強を始めたい方は、林個別指導中にお問い合わせください。
無料のオンライン体験授業も用意しております!



“高校数学B「統計的な推測」 第7章|正規分布~二項分布の近似~ やさしく解説” に対して2件のコメントがあります。
コメントは受け付けていません。